| 全文 |
一. 引言
回應本刊八十三年九月份(十八卷三期)楊維哲教授的呼籲「大學微積分的教學,
應從三向(Rule of
Three):圖像、數值、解析的全方位來進行」, 筆者甚有同感。
筆者在此願嚐試當為一個「黑手 」, 以今日電腦上最方便
(User Friendly) 的應用軟體(不需程式語言),
完全用數學觀念就可以著手進行數值演算與繪製圖像的試算表(Spread Sheets),
來達成此一有義意的工作。
在國內首創將試算表用在數學上者, 非清華大學的全任重教授莫屬,
目前筆者不僅用在微積分更頻頻應用在數值方法的教學上, 甚覺方便及實用,
在此嚐試以微積分導函數的概念及其應用為例;
設計三向教學的範例向讀者先進討教。
二. 導函數例子
(一)目 的:
幫助學生
- 建立差商及差商極限的觀念。
- 理解導函數的意義。
- 分析比較函數與其導函數間的關係。
- 了解導函數能夠分析原函數行為的功能。
(二)理 論:
- 函數 $f$ 在 $x$ 點及 $x$ 點的近傍 $x+h$ 的相關式子
$${f(x+h)-f(x)\over h}$$
謂之 $f$ 在 $x$ 點的差商。
- 函數 $f$ 在 $x$ 點的導函數 $f'(x)$ 定義為差商的極限
$$f'(x)=\lim_{h\to 0}{f(x+h)-f(x)\over h}$$
- 函數 $f$ 在 $x$ 點的導函數存在, 則謂函數 $f$ 在 $x$ 點可微分。
- 函數 $f$ 在其定義域裡每一點均可微分, 則謂 $f$ 是為可微分函數。
三. 實驗設計:
(A) 導函數是差商的極限:
- 首先將所給的函數以等間距 $x$ 點表列成表列式函數
$\forall x\rightarrow f(x)$。
- 依觀察點設定實驗區間 $[A_0,A_n]$ 及間距
$\Delta x={A_n-A_0\over n}$ 大小。
- 另外將近傍之大小也設定成可控制之變數 $h$; 以便控制觀察變因。
- 在實驗區間內的每一 $x$ 點建立函數及其差商的對應關係:
$$\forall x\rightarrow f(x)\rightarrow {f(x+h)-f(x)\over h}$$
- 另外、將函數的微分式子亦列表成表列式函數,
以便與差商極限的逼近值做比較。
- 控制並逼近 $h$ 值趨近零,
以觀察比較函數差商的變化與其微分式間的誤差關係(逼近程度)。
(B) 導函數可分析原函數的行為:
- 繪製函數 $f$ 及其導函數 $f'$ 的對應圖形, 並分析比較兩者間的變化行為。
- 縮小 $x$ 的間距大小, 進一步微觀各點近傍的函數與導函數關係。
- 變換實驗區間左端值 $A_0$ 以遍歷定義域各子區間的函數與導函數關係。
四. 實驗布局: 在 LOTUS 1-2-3 之試算表上
[註: 本文將用及如下幾則 Lotus 1-2-3 軟體上的術語]
工作底稿、圖形幕、儲存格、A欄、位址、複寫、Graph Type、
X坐標範圍、 A圖坐標範圍、巨集鍵、功能鍵;
詞意說明請參閱文後附註。
(A) 導函數是差商的極限:
(A.1) 工作底稿(參閱表 A1)
- G欄規劃為定義域; 儲存格 G1: 標記為 $x$。
- I欄規劃為 $x$之近傍; 儲存格 I1: 標記為 $x+h$。
- H欄為函數 $f$之值(形式公式); 儲存格 H1: 標記為 $f(x)$。
- E欄為對應差商值; 儲存格 E1: 標記為 D.Q。
- F欄為式的值(形式公式); 儲存格 F1: 標記為 $f'(x)$。
- A欄為實驗變數;
A1: 數值 $A_0$; 定義域上實驗區域 $[A_0,A_n]$ 的左端值,
A2:數值 $\Delta x$ ; $x$的間距大小,
A3:數值 $h$; 依實驗之進行可從0.1逐漸逼近於零,
如 0.01、0.001、...、0.00000001 等。
- B欄做為 A欄各值的標記; B1:『:A0』、 B2:『:Step』、
B3:『:h』 。
- 儲存格 G2: 直接用位址 A1引入實驗區域左端值 。
- 儲存格 G3: 以 G2為啟始點加上間距計算下一 $x$ 點的公式(+G2+$A$2)。
- G4..G60 : 複寫自 G3的步進 $x$ 點計算公式到整個觀察區間。
- 儲存格 H2: 用位址 G2為其 $x$ 值鍵入對應函數形式公式。
- H3..H60 : 複寫自 H2的函數形式公式, 建立實驗區域的值域。
- 儲存格 I2: 用位址 G2為其 $x$ 值加上近傍 $h$ 值, 建立近傍形式公式
(+G2+$A$3 ), 並複寫至 I3..I60。
- J2..J60 : 以 I欄上的對應值為自變數, 代入 H欄的函數形式公式;
即只要複寫自 H2至 H3..H60可得。
- 儲存格 E2: 對應於 G欄位上每一 $x$ 值建立差商公式, 先在儲存格
E2鍵入差商公式 (J2$-$H2)/$A$3, 然後複寫至 E3..E60。
- 儲存格 F2: 本欄是導函數形式公式(為了區別之方便,
以下將改稱為微分公式)欄, 先在此以位址 G2為自變數 $x$ 建立微分公式,
然後複寫至 F3..F60。
- 儲存格D2: 本欄是展示導函數與差商間的差距, 先在儲存格D2鍵入$x$
值的導函數與差商誤差的絕對值公式 @Abs(E2 $-$F2) 並複寫至 D3.D60。
(A.2) 圖形幕: 直觀分析比較導函數與原函數間的關係之用
- 將 Graphic Type 設定為 $XY$ 坐標形。
- 指定 $X$ 坐標範圍; 設定在 G欄位的 G2..G60。
- 指定 $Y$ 坐標範圍; 設有兩個, 其一(A圖)是原函數在 H2..H60,
另一( B圖 )是導函數在 F2..F60。
- 功能鍵 [F10] 內定為工作底稿與圖形幕間變換之用。
(A.3) 巨集鍵: 簡化更新函數用
- [1.] [Alt]+[H]: Copy 自更新函數公式之儲存格 H2 到 H3..H60。
- [2.] [Alt]+[F]: Copy 自更新微分公式之儲存格 F2 到 F3..F60。
(B)導函數可分析原函數的行為:
(B.1) 工作底稿 : 除了可刪去微分公式欄
欄位 F 欄之外, 一切同 (A.1)。
(B.2) 圖形幕: 同(A.2)。
(B.3) 巨集鍵: 同(A.3)。
五. 示範例子:
(A)認識導函數是函數之差商的極限
例A1:
試觀察函數 $f(x)=x^3+x^2+x+1$ 在範圍 $[-3,3]$ 內各點近傍的各逼近值
$(h=0.1$、$0.01$、$\cdots$、$0.00000001)$ 的差商是如何在逼近成其導函數。
實驗進行: (參閱表A1)
- 在工作底稿上將函數 $f(x)=x^3+x^2+x+1$ 布局成表列式函數。
- 在工作底稿上將導函數(為區別之方便後文將改稱為微分公式)
$f'(x)=3x^2+2x+1$ 亦布局成表列式函數。
- 取 $A_0=-3$; $\Delta x=0.1$ 觀察 $[-3, 2.8]$ 區間, 各
$x$ 值之差商的逼近情形。
- 首先取 $h=0.1$, 按巨集鍵 [Alt]$+$[H]; 複寫 H欄函數公式,
再按巨集鍵 [Alt]$+$ [F]; 複寫 F欄的微分公式。
- 這時觀察 D欄之誤差在 $0.08\lt$ Error $\lt0.8$ 之範圍內。
- 當取 $h=0.01$ 時誤差變為 $0.001\lt$ Error $\lt0.095$ 之範圍。
- 當取 $h=0.001$ 時誤差變為 $0.002\lt$ Error $\lt0.009$ 之範圍。
- 當取 $h=0.001$ 時誤差變為 $0.00940\lt0.2680 $ 之範圍 o
- 當繼續縮小近傍的間距 $h$ 至 $h=10^{-8}$ 則誤差範圍亦相對的縮小到
$7.150\times 10^{-11}\lt$ Error $\lt3.309\times 10^{-7}$。
- 繼續取 $A_0=2.8$; $\Delta x=0.1$
再觀察 $[2.8, 8.6]$ 區間, 各 $x$ 值之差商的逼近情形。 %9
- 當取 $h=0.1$ 時誤差為 $0.95\lt$ Error $\lt2.69$ 之範圍。
- 當取 $h=0.001$ 時誤差為 $0.00940\lt$ Error $\lt0.2680$ 之範圍。
- 當繼續縮小近傍的間距 $h$ 至 $h=10^{-8}$ 則誤差範圍亦相對縮小到
$2.9\times 10^{-8}\lt$ Error $\lt2.128\times 10^{-5}$。
- 同樣的將區間移至右翼, 取 $A_0=-8.8$; $\Delta x=0.1$ 進一步觀察 $[-8.8,
-3]$ 區間各 $x$ 值之差商的逼近情形。
- 當取 $h=0.1$ 時誤差為 $0.79\lt$ Error $\lt2.53$ 之範圍。
- 當取 $h=0.01$ 時誤差為 $0.079\lt$ Error $\lt0.2539$ 之範圍。
- 再繼續縮小近傍的間距 $h$ 至 $h=10^{-8}$ 則誤差範圍亦相對縮小到
$4.39\times 10^{-8}\lt$ Error $\lt1.2875\times 10^{-5}$。
- 綜合上述三段範圍的實驗觀察得在區間 $[-8.8, 2.8]$ 內, 當各 $x$
點之近傍從 $h=0.1$ 縮小至
$h=10^{-8}$ 時 $x$ 點的差商與微分公式值間的誤差也是從
$0.95\lt$ Error$ \lt 2.65$ 的範圍縮小到
$4.39\times 10^{-8}\lt$ Error $\lt2.128\times 10^{-5}$
的範圍。
| A | B | D | E | F | G | H | I |
| 1 | -3.0000 | :A0 | Error | D.Q | f'(x) | x | f(x) | x+h |
| 2 | 0.1000 | :Step | 0.7900 | 21.2100 | 22.0000 | -3.0000 | -20.0000 | -2.9 |
| 3 | 0.1000 | :h | 0.7600 | 19.6700 | 20.4300 | -2.9000 | -17.8790 | -2.8 |
| 4 | | | 0.7300 | 18.1900 | 18.9200 | -2.8000 | -15.9120 | -2.7 |
| 5 | | | 0.7000 | 16.7700 | 17.4700 | -2.7000 | -14.0930 | -2.6 |
| 6 | | | 0.6700 | 15.4100 | 16.0800 | -2.6000 | -12.4160 | -2.5 |
| 7 | | | 0.6400 | 14.1100 | 14.7500 | -2.5000 | -10.8750 | -2.4 |
| 8 | | | 0.6100 | 12.8700 | 13.4800 | -2.4000 | -9.4640 | -2.3 |
| 9 | | | 0.5800 | 11.6900 | 12.2700 | -2.3000 | -8.1770 | -2.2 |
| 10 | | | 0.5500 | 10.5700 | 11.1200 | -2.2000 | -7.0080 | -2.1 |
| 11 | | | 0.5200 | 9.5100 | 10.0300 | -2.1000 | -5.9510 | -2.0 |
| 12 | | | 0.4900 | 8.5100 | 9.0000 | -2.0000 | -5.0000 | -1.9 |
| 13 | | | 0.4600 | 7.5700 | 8.0300 | -1.9000 | -4.1490 | -1.8 |
| 14 | | | 0.4300 | 6.6900 | 7.1200 | -1.8000 | -3.3920 | -1.7 |
| 15 | | | 0.4000 | 5.8700 | 6.2700 | -1.7000 | -2.7230 | -1.6 |
| 16 | | | 0.3700 | 5.1100 | 5.4800 | -1.6000 | -2.1360 | -1.5 |
| 17 | | | 0.3400 | 4.4100 | 4.7500 | -1.5000 | -1.6250 | -1.4 |
| 18 | | | 0.3100 | 3.7700 | 4.0800 | -1.4000 | -1.1840 | -1.3 |
| 19 | | | 0.2800 | 3.1900 | 3.4700 | -1.3000 | -0.8070 | -1.2 |
| 20 | | | 0.2500 | 2.6700 | 2.9200 | -1.2000 | -0.4880 | -1.1 |
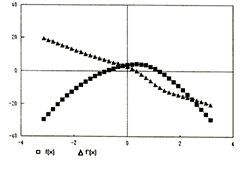 圖 A2
圖 A2
例A2:
試觀察函數 $f(x)\!=\!e^{\sin x+\cos x}$ $-\pi x^2+1$ 在範圍
$[-\pi,\pi]$ 內各 $x$ 近傍的各逼近值
($h=0.1$、$0.01$、$\ldots$、$0.00000001$) 的差商是如何逼近成其導函數。
實驗進行: (參閱圖A2)
- 取間距大小 Step=@pi/18 $(\Delta={\pi\over 18})$。
- 將函數 $f(x)=e^{\sin x+\cos x}-\pi x^2+1$ 布局成表列式函數:
@exp(@Sin(G2) $+$@Cos(G2)) $-$@pi*G2^2+1。
- 亦將其函數的微分式子 $f'(x)=$ $e^{\sin x+\cos x}(\cos x-\sin x)-
2\pi x$ 布局成表列式函數: @exp(@Sin(G2)+@Cos(G2)) $*$(@Cos(G2)
$-$@Sin(G2))$-$ 2 $*$@pi $*$G2。
- 取 $A_0=-\pi$ 先觀察 $[-\pi,0]$
區間, 各 $x$ 值之差商逼近其導函數值的情形。
- 當近傍 $h\!=\!0.1$ 時差商誤差值在 $0.207233\lt$ Error $\lt0.328287$
之範圍內。
- 當近傍 $h\!=\!0.01$ 時差商誤差值在 $0.020609\lt$ Error $\lt0.0315524$
之範圍內。
- 當近傍 $h\!=\!0.001$ 時差商誤差值在 $0.00206017\lt$
Error $\lt0.00314295$ 之範圍 內。
- 當近傍 $h\!=\!10^{-9}$ 時差商誤差值在
$0.36\times 10^{-8}\lt$ Error $\lt0.42861\times 10^{-5}$ 之範圍內。
- 取 $A_0\!=\!0$ 再觀察 $[0,\pi]$ 區間上各 $x$ 值之差商的逼近情形(表 1-2)。
- 當近傍 $h\!=\!0.1$ 時差商誤差值在 $0.205665\lt$ Error $\lt0.602379$
之範圍內。 %10
- 當近傍 $h\!=\!0.01$ 時差商誤差值在 $0.0209038\lt$ Error $\lt0.0599666$
之範圍內。
- 當近傍 $h\!=\!0.001$ 時差商誤差值在 $0.002060023\lt$ Error $\lt0.00599284$
之範圍內。
- 當近傍 $h\!=\!10^{-9}$ 時差商誤差值在 $0.9\times 10^{-9}\lt$ Error
$\lt0.32857\times 10^{-5}$ 之範圍內。
- 綜合上述二段的實驗觀察得在區間 $[-\pi,\pi]$
內, 當各 $x$ 之近傍從 $h\!=\!0.1$ 縮小至
$h\!=\!10^{-9}$ 時 $x$ 點的函數差商與其微分公式的實際值間誤差也從
$0.207233\!\lt$Error$\lt\!0.602379$ 的範圍縮小到
$0.36\times 10^{-8}\!\lt$Error$\lt\!0.42861\times 10^{-5}$ 的範圍。
(B) 理解導函數可分析原函數之行為
例B1:
試觀察函數 $f(x)=x^2+x+1$
在範圍 $[-3, -3]$ 內, 各 $x$ 點所對應函數與導數間行為的相應變化關係。
實驗進行: (參閱圖B1)
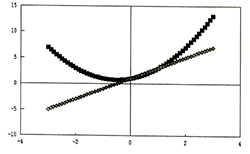 圖 B1
圖 B1
- 在A1實驗布局中刪除或忽視本實驗不用的欄位; D誤差及 F微分公式欄。
若重新布局則先設定觀察區間 $x$ 值範圍; 即設定 $A_0$ 及 $\Delta x$ 值,
並表列函數 $f(x)$ 及其差商在工作底稿上即可。
- 設定近傍 $h\!=\!0.000001$ 則依前例 A1 所做的實驗其導函數的誤差應會小於
0.000001。
- 當取 $A0\!=\!-3$ 及 Step$=\!0.1$ 觀察並比較工作底稿上的導函數(E欄)及函數
(H欄)。
- 在 $x\!\lt\! -0.5$; i.e $[-3,-0.5]$ 範圍內, 導函數值為負, 而在
$x \!>\! -0.5$; i.e $[-0.5, 3]$ 範圍內, 導函數值為正。
- 相應於上述兩區間的函數變化行為則有在
$[-3,-0.5]$ 範圍內, 函數值從 7遞減到 0.75, 但在
$[-0.5, 3]$ 範圍內, 函數值從 0.75 遞增到 13。
- 也就是, 在點 $x\!=\!-0.5$ 對函數及導函數恰好都是分水嶺,
對函數而言, 這一點正好是從減函數變換到增函數的變換點,
對導函數而言, 這一點正好是從負值變換到正值的轉換點。
- 進一步的按一下[F10]再看一看圖形, 顯然的原函數是開口向上的拋物線,
最低點正是在 $x\!=\!-0.5$ 的地方。
- 其次, 看一看導函數, 這是一條傾斜的直線, 而正也是在 $x\!=\!-0.5$
的地方與 X 軸相交。
- 比較函數與導函數兩者間行為變化的關係, 發現以點 $x\!=\!-0.5$ 為分水嶺。
在$[-3,-0.5]$ 範圍, 函數是遞減而導函數值則是負值,
在 $[-0.5, 3]$ 範圍, 函數是遞增而導函數值則是正值。
例B2:
試觀察函數 $f(x)\!=\!e^{\sin x+\cos x}\!-\!\pi x^2\!+\!1$ 在範圍 $[-\pi,\pi]$
內, 各 $x$ 點所對應函數與導函數間行為的相應變化關係。
實驗進行: (參閱圖B2)
 圖 B2
圖 B2
- 在例B2的實驗布局上, 將函數 $f(x)$ 更改為
@exp(@Sin(E2) $+$@Cos(E2)) $-$@pi $*$E$\wedge 2 +1$
並按巨集鍵[Alt]+[H]以完成表列式函數之布局。
- 當取 A0$=-$@pi (i.e$-\pi)$ 及 Step=@pi/30(i.e${\pi\over 30}$)
觀察並比較導函數(E欄)及函數(H欄)。
- $x$ 在 $[\pi,0.314159]$ 範圍內, 導函數值是正數,
相對應的在 H欄的原函數是從 $-29.6383$ 遞增到 4.215617。
- 同樣在這 $x$ 的範圍內, 另外看到導函數是從 19.37132遞減到 0.289705,
所以進一步的按功能鍵[F10]看一看圖形,
在這兒可以看到由於其變化率的遞減而原函數圖形的凹性向下行為。
- 更且, 其導函數並不若例A1二次錐線的導函數是為直線, 而有點彎彎曲曲,
所以原函數圖形雖然看起來很像拋物線, 但實際上不是, 尤其在範圍
$[-1,0]$ 的區間, 導函數的遞減程度是緩慢下來, 而原函數的陡峭也就緩和下來,
在這兒曲線似乎沒有如拋物線的穩定爬升。
- $x$ 在 $[0,\pi]$ 的範圍內, 導函數值則從正數遂漸減少經點 $x\!=\!0.314159$
轉變成負數, 相對於在 H欄的原函數是慢慢增大跨過最大值 4.215617再慢慢減小成零,
再一路快速遞減到 $x=\pi$ 時的 $-29.6383$。
- 同樣在這 $x$ 的範圍內, 另外看到導函數是從2.71828遞減到零,
再繼續快速減少到最右端時的 $-20.1070$。
- 另一面, 進一步按功能鍵[F10]看一看圖形,
這一段範圍的導函數圖形是向右傾斜向下是彎彎曲曲近似於直線的曲線,
這表示導函數的遞減率是在急速減少, 所以原函數圖形正也表現出凹性向下之行為。
例B3:
試觀察函數 $f(x)=x^3-5x-20$ 在範圍 $[-3,3]$ 內, 各 $x$
點所對函數與導函數間行為的相應變化關係。
實驗進行: (參閱圖B3)
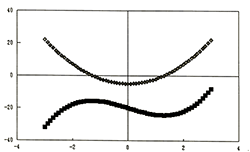 圖 B3
圖 B3
- 同在例 B1 工作底稿的實驗布局上, 將函數 $f(x)$ 更改為
G2$\wedge$ 3$-$5$*$G2$-$20 並按巨集健[Alt]+[H]以完成表列式函數之布局。
- 當取 A0$=-3$ 及 Step$=0.1$ 的情況下, 觀察並比較工作底稿 E
及 H兩欄的關係。
- $x$ 在 $[-3, -1.3]$ 範圍內, 導函數是正數, 相應的在 H欄上的原函數值是從
$-32$ 遞增到 $-15.697$。
- $x$ 在 $[-1.2, 1.2]$ 的範圍內, 導函數是負數, 相應的在 H欄上的函數值是從
$-15.728$ 遞減到 $-24.272$。
- $x$ 在 $[1.3, 3]$ 的範圍內, 導函數是正數, 相應的在 H欄的函數值是從
$-24.303$ 遞增到 $-8$。
- 另一方面, 按功能鍵[F10]看一看圖形幕, 相同於 $3^\circ,4^\circ,5^\circ$
在 $[-3, -1.3]$ 區間, 導函數圖形在 X軸上方, 而原函數圖形則是遞增,
在 $[-1.2, 1.2]$ 區間, 導函數圖形在 X軸的下面, 而原函數圖形則是遞減,
在 $[1.3, 3]$ 區間, 導函數圖形在 X軸上方, 而 原函數圖形則是遞增。
- 對於導函數圖形與 X軸有兩交點, 其一在 $x=-1.3$, 另一在
$x=1.3$, 這兩點從工作底稿的函數表列上, 看到其函數值
$f(-1.3)=-15.697$ 較其近傍大, 而
$f(1.3)=-24.303$ 則較其近傍小, 在圖形幕上的圖形也正具相同的特徵;
點 $(-1.3, -15.697)$ 是相對極大, 而點 $(1.3, -24.303)$ 則是相對極小。
- 再看一看導函數圖形, 在 $[-3, 0]$ 範圍內, 導函數圖形是遞減,
相應的函數的彎曲程度, 從左端點開始向右逐漸變小, 而在
$[0, 3]$ 的範圍內, 導函數圖形是遞增, 相應的函數圖形的彎曲程度, 從
Y軸的交點開始向右逐漸變大, 而最特別的是在 Y軸上,
導函數圖形恰是從遞減變成遞加的變換點,
相應的函數圖形在這一點恰是凹性向下的圖形轉變成凹性向上的圖形。
六. 實驗結果:
(A)函數是差商的極限:
- 這裡所舉的兩例是一般的連續函數; 其一是多項函數, 另一是超越函數。
- 在指定區間上各 $x$ 點, 雖然是取間距點而非連續, 但在 $x$ 間的間距
$\Delta x$ 大小是為實驗變數; 可任意變換所以並不失去連續的一般性而可繼續追蹤。
- 在這實驗裡各 $x$ 點的近傍 $h$ 雖用十分逼法,
但這也是實驗變數,故可選用任意的逼近數值來趨近, 其結果一樣也不失其一般性。
- 在這實驗所看到現象正如理論所言「函數
$f$ 在 $x$ 點的導函數恰為此點上的差商在其近傍逼近零時的極限值」。
- 在這實驗裡對每次的實驗變數變換均可看到差商在於逼近其微分公式值間的誤差逼近程度。
(B)導函數可分析原函數的行為
- 這裡所舉的例 B2是同為(A)所舉之例 A2是為超越函數。
- 不論原函數是多項函數或超越函數,
從數值表列導函數的符號變化均可以推測原函數的增減函數關係。
- 同樣的, 這三種函數從函數圖形上, 更清楚的可以看出當導函數圖是在 X軸
以下部分的區間, 原函數圖必是從左到右之遞減曲線, 也就是減函數圖形。
- 導函數變號的交換點, 顯然是原函數的遞增與遞減或遞減與遞增的交接點,
所以在圖形上所看到的這些點必定是相對極點(Relative Extreme Point)。
- 另外, 在例 B3 看到了導函數值是零的點並不一定是相對極點, 這是當導函數值,
從正變零而不進入負值又變回正值時, 或從負變零而不進入正值又變回負值的情況,
這正是反曲點(Inflection Point)的現象。
- 同時, 在例 B3 的圖形上也看到了反曲點的兩翼,其曲線的凹向性恰好是相反。
七. 結論
從上述的設計例子, 以今日電腦科技, 要達成微積分三向方式的教學,
在工具方面己唾手可得, 所缺的應只是有心的「黑手」。
然而較為讓人所擔心的是目前所盛行的 CAI 方式。這方式的設計若不小心,
那麼學生學到的將是欠缺數學思考的速查電子解答習慣, 這對微積分三向教學並無助益。
使用的軟體方面, 當然也可以用程式語言來設計, 但這將花費相當的時間、勞力及精力,
因而降低了學習的效力。況且數學觀念的學習, 絕大部分可透過函數觀念獲得的,
所以電子試算表不失為一個相當理想的輔助工具。今日的電子試算表在市面上不只是
LOTUS1-2-3, 其他尚有 Excel、 Symphony、 Quattro、 Karuku(日文)等多種,
也都是非常簡單好用。筆者在此拋磚引玉,
配合楊教授的呼籲與各位讀者先進, 不恥隨時降格為「黑手」,
來推展這一有意義之教學方法。
附註:
- 工作底稿 :
一張具有橫寬256行, 縱長8192列的電子試算表。
- 圖形幕 :
可將工作底稿上的資料表成 $XY$ 坐標或統計圖形的電子幕。
- 儲存格 :
工作底稿上所規劃出來的格子, 共有256$\times$8192格,
是存放及顯示資料的單位格子; 本文的敘述是以這格子為單位,
放入了各變數值及公式。
- A欄 :
工作底稿上的256行的各行是用英文字母A..Z、AA..IV來表示,
所以第一行的整行叫做 A欄、第二行叫 B欄等等。
- 位址 :
各儲存格位置的形式表示法, 以各欄位的第幾個格子來表示, 如 B
欄位的第三個格子表之以 B3。
- 複寫(Copy):
這是 Lotus 1-2-3 試算表所提供之功能指令,
選用這一指令可將某一儲存格上的公式,
依相對的變數位址複寫到指定的儲存格範圍內。
- Graph Type :
Lotus 1-2-3 所提供可在圖形幕上展現的圖形;
有統計上的折線圖、長條圖、疊積圖、圓形圖及本文所用的 $XY$ 坐標圖。
- $X$ 坐標範圍 :
圖形幕是基於展現在工作底稿上的資料來繒製的,
所以要求繒圖之預前工作除指定 Graph Type之外,
還要指定橫坐標的資料在工作底稿上的所在範圍。
- A 坐標範圍 :
圖形幕上在同一 $X$ 坐標範圍下可指定 A、B、C、D、E、F
之六個圖形; 因此在繒圖之預前工作, 也須指定工作底稿上縱坐標資料之所在範圍。
- 巨集鍵 :
使用者依自已之須要設定的按健, 在本軟體規定使用[Alt]
及另一個英文字母同時並用, 這是替代一群指令的組合,
只用一次簡單的按健就可完成; 如本文用了兩個巨集健,
其中 [Alt]+[H]定義為將位址 H2 上的函數公式複寫到
H3..H62及 J2..J60 以便更新指定範圍內的表列式原函數及近傍函數,
另一[Alt]+[F]定義為將位址 F2上的微分公式複寫到F3..F62
以便更新微分式子。
- 功能鍵 :
這是鍵盤上 F1..F12的特殊功能鍵, Lotus 1-2-3 定義[F10]
做為工作底稿與圖形幕間兩者變換的開關。
參考資料
- Simon Moores; Using Lotus 1-2-3 Release 3.0。
- Ridington Tucker; Inside Lotus 1-2-3 Macro。
- 微積分教本。
---本文作者任教於彰化師範大學數學系---
|





