| 發刊日期 |
2023年6月
|
|---|---|
| 標題 | 利用切線段的總長建構弧長的上和 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
在微積分的教學中, 通常使用上和、下和(upper sum, lower sum), 以夾擠的方式來定義面積。 但是對弧長, 卻只用下和, 以最小上界的概念來定義(註一)。 本文嘗試利用切線段賦予凹口向下或向上的函數圖形的弧長一個上和的設計, 並說明此一上和與原來的下和亦可夾擠得到弧長。本文共分四節, 第一節複習上和、 下和、 黎曼和及面積, 第二節複習弧長的下和, 第三節引入弧長的上和, 第四節是一個簡要的回顧。 第一節 上下和與面積微積分對一個連續函數 $y=f(x)$ 在閉區間 $[a,b]$ 上函數圖形與 $x$-軸所決定的面積, 通常是以上和及下和的極限來表示。 質言之, 如下圖一, 如果暫時假設連續函數 $f(x)$ 在 $[a,b]$ 上大於 0, 則將 $[a,b]$ 分成若干段, 稱為分割 (partition), 並且在每一分割段上取 $f(x)$ 的最大值和最小值。
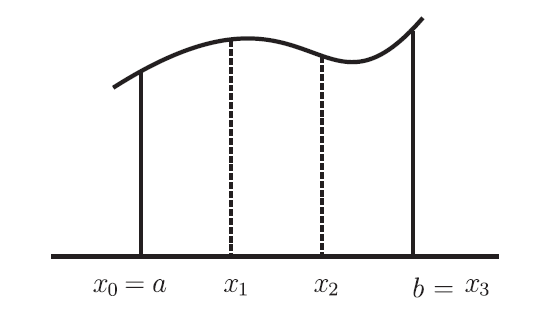
以 $[a,b]$ 分成三段為例, 則 \begin{align} \hbox{上和}=\,&(x_1-x_0 ) M_1+(x_2-x_1 ) M_2+(x_3-x_2 ) M_3,\label{1}\\ \hbox{下和}=\,&(x_1-x_0 ) m_1+(x_2-x_1 ) m_2+(x_3-x_2 ) m_3;\label{2} \end{align} 式中, $M_i$ 及 $m_i$ 分別表示第 $i$ 分段上的最大值和最小值。 另外, 又有黎曼和, 它是指在第 $i$ 分段中, 任取一個函數值 $f(z_i)$ 而寫下 \begin{align} \hbox{黎曼和}=(x_1-x_0 )f(z_1)+(x_2-x_1 )f(z_2)+(x_3-x_2 )f(z_3);\label{3} \end{align} 式中, $x_{i-1}\le z_i\le x_i$。 為了簡化說明, 不妨取 $[a,b]$ 的 $n$ 段等分割, 則 $x_i-x_{i-1}=\dfrac{b-a}n$, 當 $n\to\infty$ 時, 上和、 下和及黎曼和均有相同的極限, 此一極限就是(或定義為) $f(x)$ 在 $[a,b]$ 上與 $x$-軸所決定的面積, 記為 $\displaystyle\int_a^b f(x) dx$。(註二) 我們注意到對同一分割上和$\ge $黎曼和$\ge $下和, 而對連續函數而言, 當 $n\to\infty$ 時單獨只考慮上和或下和就能得出極限 $\displaystyle\int_a^bf(x) dx$。(註三) 第二節 以下和方式定義弧長如果 $y=f(x)$ 在 $[a,b]$ 這一段可以微分, 並且 $f'(x)$ 連續, 如圖二所示。
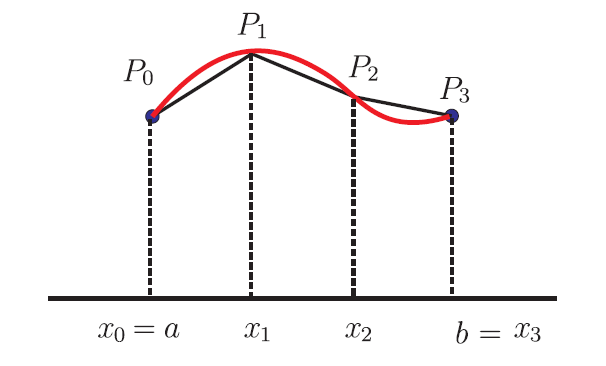
將 $[a,b]$ 分成若干段 (例如, 圖二中的三段), $x_0=a\lt x_1\lt x_2\lt x_3=b$。 在圖形上對應的點分別是 $P_0,P_1,P_2,P_3$。 將這些點依序連成折線, 則這些折線的總長就是一個弧長的下和。 一般微積分課本對弧長的定義是取所有這些可能的下和的最小上界。(同註一) 在計算時, 考慮一段 $P_{i-1} P_i$,
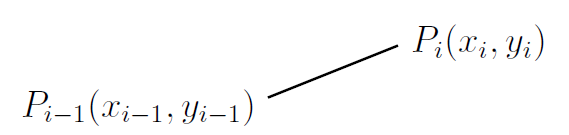
其長度是 \begin{align} [(x_i-x_{i-1} )^2+(y_i-y_{i-1} )^2 ]^{\frac 12}=(x_i-x_{i-1} ) \left[1+\Big(\frac{y_i-y_{i-1}}{x_i-x_{i-1}}\Big)^2 \right]^{\frac 12}.\label{4} \end{align} 由中值定理(mean value theorem) $$\frac{y_i-y_{i-1}}{x_i-x_{i-1}}=f' (z_i ),\quad x_{i-1}\le z_i\le x_i.$$ \eqref{4} 式變成 \begin{align} (x_i-x_{i-1} ) \left[1+\big(f' (z_i )\big)^2 \right]^{\frac 12}.\label{5} \end{align} 將 \eqref{5} 對 $i=1,2,\ldots,n$ 求和得到函數 $y=(1+f' (x)^2 )^{\frac 12}$ 的一個黎曼和, 若分段越細, 再取極限就會得到 $$ \int_a^b\Big(1+f'(x)^2\Big)^{\frac 12} dx.$$ 此即微積分課所談論函數 $y= f(x)$ 圖形的弧長公式。 注意到 \eqref{5} 所得到的黎曼和均小或等於弧長, 是所謂下和。 第三節 以上和方式定義弧長如果要定弧長的上和, 先得假設 $y=f(x)$ 的圖形在 $[a,b]$ 上凹口向下或向上 (concave), 此處, 不妨設圖形是凹口向下或假設 $f''$ 在 $[a,b]$ 上小於 0, 如圖三, 仍以 $[a,b]$ 的三分段為例
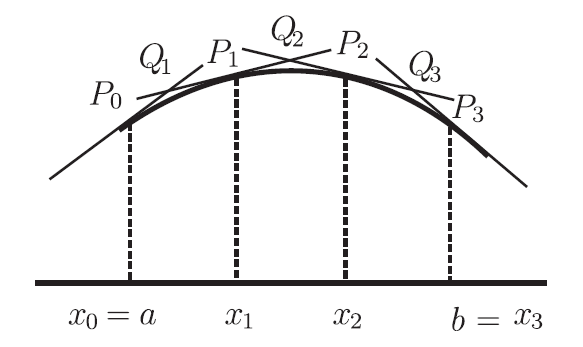
我們在 $P_0,P_1,P_2,P_3$ 分別作 $y=f(x)$ 圖形的切線, 這些切線依序交於 $Q_1,Q_2,Q_3$, 則 $\overline{P_0Q_1}+\overline{Q_1Q_2}+\overline{Q_2Q_3}+\overline{Q_3P_3}$ 就是弧長的一個上和。(註四) 原因是根據三角形兩邊和大於第三邊, $$\overline{P_0Q_1}+\overline{Q_1Q_2}+\overline{Q_2Q_3}+\overline{Q_3P_3}\ge \overline{P_0P_1}+\overline{P_1P_2}+\overline{P_2P_3},$$ 所以上和當然大或等於弧長 對圖形外切折線段的和, 我們有下列的公式, 如圖四 設 $P_{i-1}=(x_{i-1},y_{i-1} )$, $Q_{i-1}=(u_{i-1},v_{i-1} )$, $Q_i=(u_i,v_i )$
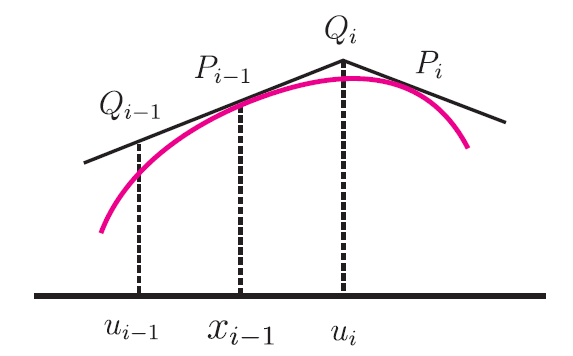
則線段 $Q_{i-1} Q_i$ 的長是 $$\big((u_i-u_{i-1})^2+(v_i-v_{i-1} )^2 \big)^{\frac 12}=(u_i-u_{i-1} ) \left(1+\Big(\frac{v_i-v_{i-1}}{u_i-u_{i-1}}\Big)^2 \right)^{\frac 12}.$$ 但 $\dfrac{v_i-v_{i-1}}{u_i-u_{i-1}}$ 是 $Q_{i-1} Q_i$ 的斜率, 亦即 $f' (x_{i-1} )$。 所以 $Q_{i-1} Q_i$ 的長是 \begin{align} &\hskip -20pt (u_i-u_{i-1}) \big(1+f'(x_{i-1} )^2 \big)^{\frac 12}.\label{6}\\ {\hbox{而 }} Q_1 P_0=\,&\big((u_1-x_0 )^2+(v_1-y_0 )^2 \big)^{\frac 12}\nonumber\\ =\,&(u_1-x_0 ) \left(1+\Big(\frac{v_1-y_0}{u_1-x_0}\Big)^2 \right)^{\frac 12}\nonumber\\ =\,&(u_1-x_0 ) (1+f'(x_0 )^2 )^{\frac 12}.\label{7} \end{align} 將 \eqref{6} \eqref{7} 諸式加總得 \begin{align} &\hskip -20pt (u_1-x_0 ) \big(1+f' (x_0 )^2 \big)^{\frac 12}+(u_2-u_1 ) \big(1+f' (x_1)^2 \big)^{\frac 12}+\cdots\nonumber\\ &+(u_n-u_{n-1} ) \big(1+f' (x_{n-1} )^2 \big)^{\frac 12}+(x_n-u_n ) \big(1+f' (x_n )^2 \big)^{\frac 12}.\label{8} \end{align} 對應 $a=x_0\lt u_1\lt u_2\lt\cdots\lt u_n\lt b=x_n$ 的分割, \eqref{8} 式恰是此分割的一個黎曼和。 當然在分割越細後, 會得到極限 $\displaystyle\int_a^b\!\!\sqrt{1+f' (x)^2}\, dx$。 第四節 回顧在第三節處理弧長的上和時, 我們圖形局限在下凹(或上凹)的情形, 原因是當 $f''\lt0$ (下凹)時, $f'$ 遞減, 如圖五
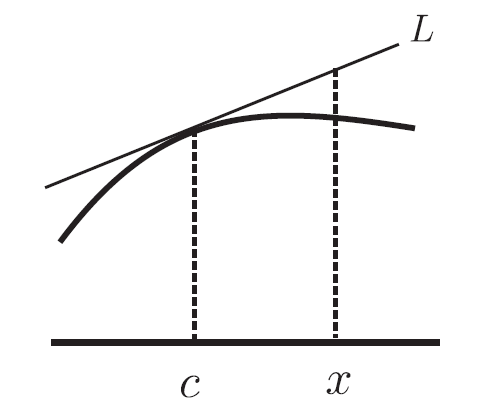
我們可以證明圖形會在過 $(c,f(c))$ 切線的下方。 證明如下: 切線 $L$ 的方程式為 $L(x)=f(c)+f' (c)(x-c)$, 考慮 $L(x)-f(x)$, 則 $L(c)-f(c)=f(c)-f(c)=0$, 而 \begin{align} L'(x)-f'(x)=f'(c)-f'(x).\label{9} \end{align} 當 $x\gt c$ 時, \eqref{9} 式為正, $x\lt c$ 時, \eqref{9} 式為負, 因此 $L(x)-f(x)$ 在 $x\gt c$ 遞增, 在 $x\lt c$ 遞減, 加上 $L(c)=f(c)$ 因此 $x\not= c$ 時 $L(x)\gt f(x)$。 正因為 $y=f(x)$ 的圖形在切線的下方, 我們才有圖三、 圖四。 圖四中過 $P_{i-1}$ 和過 $P_i$ 的切線在 $P_{i-1}$ 和 $P_i$ 之間相交(於 $Q_i$)。 若不固定凹向, 以函數 $g(x)=x(x-1)(x+1)$ 為例, 圖形如圖六
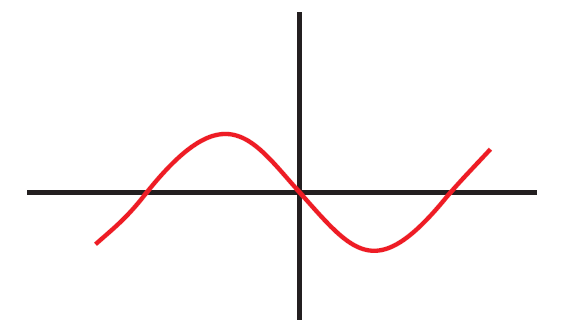
$y=g(x)$ 圖形的反曲點在原點, 並以原點為對稱中心, 即圖形繞原點旋轉 $180^\circ$°, 圖形不變。 如此一來, 如圖七

在大於 0 時是上凹, 在小於 0 時是下凹, 而在 $x$ 和 $-x$ 的切線互相平行, 無法像圖四中有切線相交的現象。 不過, 弧長本來就如面積一樣是有可加性的, 因此可以分成上凹與下凹區域來討論, 以圖六為例, 如果在下凹區 $[-1,0]$ 得到弧長為 $\displaystyle\int_{-1}^0\sqrt{1+f' (x)^2}dx$ 而在上凹區 $[0,1]$ 得到弧長為 $\displaystyle\int_0^1\sqrt{1+f' (x)^2}dx$, 則同樣得到從 $x=-1$ 到 $x=1$ 的弧長公式是 $\displaystyle\int_{-1}^0+ \int_0^1= \displaystyle\int_{-1}^1\sqrt{1+f' (x)^2}\,dx.$ 註一、 請參考(例如) Adams 與 Essex 所編微積分 8 版 (頁 405) 以所有下和的最小上界定義弧長。 註二、 如果 $f(x)$ 有正有負, (1)、 (2)、 (3) 式仍然一樣定義, 但極限所得的 $\displaystyle\int_a^bf(x) dx$ 不一定為正。 註三、 上和 $\ge \displaystyle\int_a^b f(x)dx\ge $ 下和, 形式上類似夾擠定理 (Squeeze Theorem)。 註四、 回顧對圖周長的討論, 本來就有兩種方式, 內接正 $n$ 邊形或外切正 $n$ 邊形, 如圖所示。
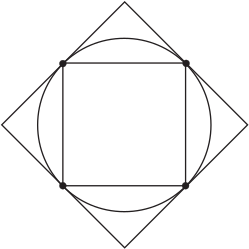
外切折線的和是圓周長之上和, 內接是下和。 本文作者為台大數學系退休教授 |
2023年6月 47卷2期
利用切線段的總長建構弧長的上和

