| 發刊日期 |
2024年12月
|
|---|---|
| 標題 | 以數學理解世界 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
2024年院區開放 統計與機率是什麼? 統計與機率當然就是在講: 當你有很多很多數據的話, 你覺得它的行為會是什麼? 或者是, 我們怎麼樣從很多數據裡面得到一些資訊。 為什麼我要把它改成放在第一個講? 它其實和數學的歷史是很不相容的, 因為數學的歷史不是從這個開始。 I. 統計與機率雖然很多研究都指出: 人類可能天生就有對數字的感覺, 所以數學的歷史是從數數開始的; 就像小 baby, 歷史介入數學也是從一二三四五六這樣開始。 但是普遍來講, 人類好像對很大的數字, 會感到難以理解, 沒有那種直覺。 但是偏偏到處都有數據, 這對於理解現在的社會是不可或缺的工具。 所以我想第一個拿出來講的就是統計, 希望國、 高中的數學裡面, 教育裡面也可以,納入越來越多統計的概念。   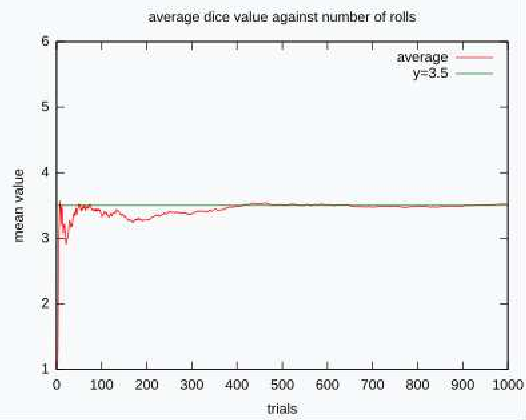 統計我們回來再講: 統計是什麼? 我剛剛講說: 統計其實就是關於很多很多的數字, 很大的數字, 所以統計的開端是從白努利的大數法則開始。 這大概是 18 世紀的事情, 已經蠻晚近了。 這個白努利和物理學的白努利, 不是同一個白努利, 他們一家都是天才, 他們好像是舅甥的關係之類的。 他發現的一個法則, 就是你的樣本數、 抽樣的數量越多, 它的平均值就有越高的可能來接近期望值。 那麼什麼是期望值? 你可以把它想成是一個理論上的平均值。 例如說, 你今天丟骰子, 骰子有 6 面 1, 2, 3, 4, 5, 6, 如果這骰子是公平的, 你丟下去每一面出現的機率都是一樣的, 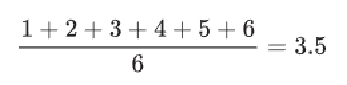 對不對? 所以它的理論上的平均值就是這個算式 $\frac {1+2+3+4+5+6}6$ 算出來的 3.5, 對不對? 可是你丟一次骰子不可能丟出來 3.5, 丟兩次可能是 1 和 2, 平均也不是 3.5, 難道這期望值的平均值, 理論平均值是錯的嗎? 不是。 我們都知道玩過骰子的人都知道, 你要丟很多次, 越來越多次, 它的平均值就真的會跟理論的平均值一樣, 這就是白努利發現的事情, 花了人類可能幾千幾千年才歸納出這樣子的一個規律。 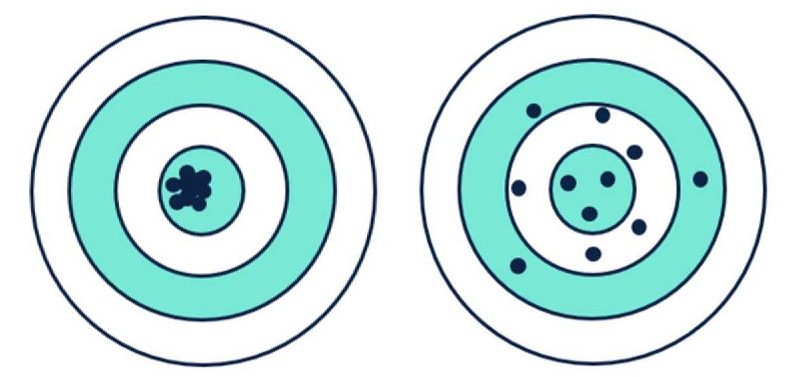 除了平均值之外, 我們還知道數據的變異性有多大。 什麼叫變異性呢? 像你看這兩張圖就知道, 它們的平均值都是在最中間。 左邊這樣子的, 我們就說它變異數比較小; 右邊就是有很多異類的, 我們說它的變異數很大。 我們再想想, 如果你有發明一種新的骰子, 它有三面是 3, 三面是 4, 所以它的平均值是不是和普通的正常的骰子一樣是 3.5? 但是你後來新發明的那種奇怪的骰子, 變異數就比較小, 因為你骰出來不是 3 就是 4, 都很靠近平均值。 正常的骰子骰出來可能是 1, 2, 3, 4, 5, 6, 雖然平均出來是一樣的數字, 但它有很多異類, 屬於像右邊的那樣狀況, 變異數很大。 這就是平均值跟變異數, 是在數據裡面對我來講最重要的兩個數。 我們常常在講常態分布, 大家都聽過它, 那麼常態分布到底是什麼?常態分布, 又或者叫做鐘形曲線, 它就是長成這樣子一個的分布。它的變異數就是紅色這一條。 所以常態分布越肥, 它的變異就越大;常態分布越尖, 它的變異就越小。 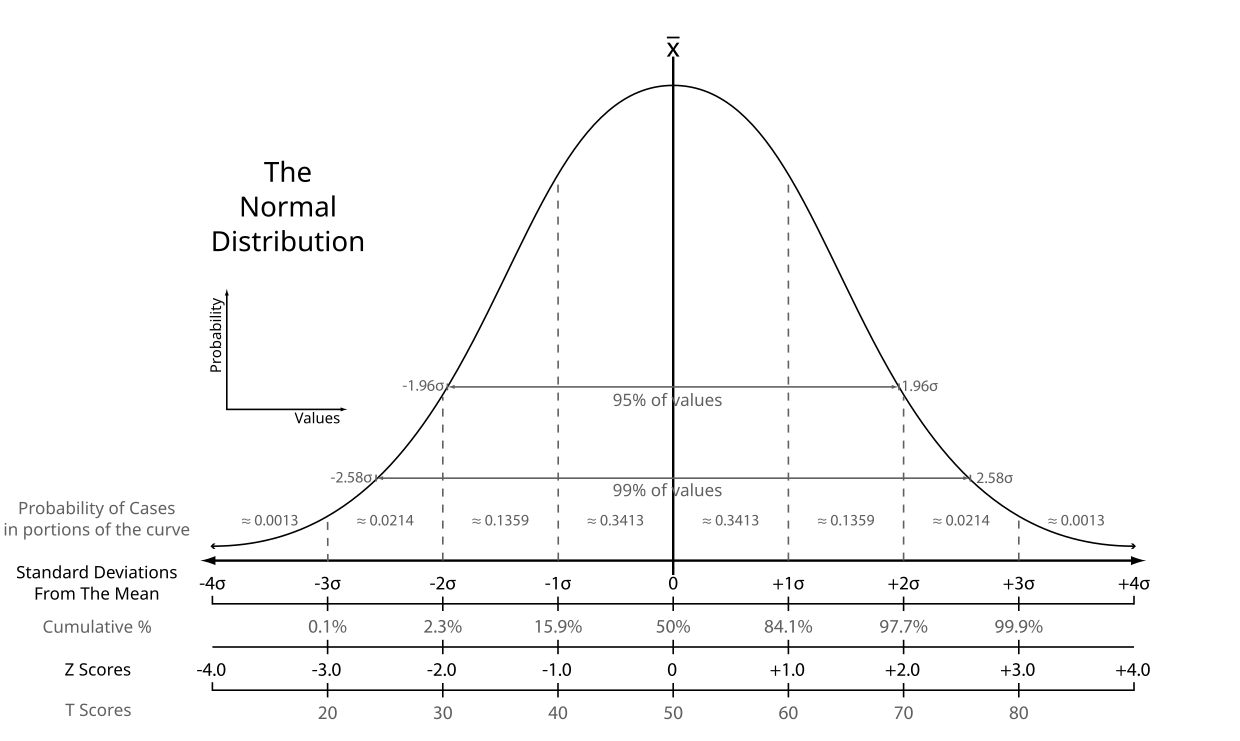 為什麼我們要一直講常態分布? 到底是為什麼? 這也是來自數學, 它背後的原因就是所謂的中央極限定理, 它在講什麼? 它在講的就是說: 平均下來, 我們都很常態, 我們都很正常。 那是什麼意思呢? 你們要看的話, 可以看定理的內容, 或者是可以先從例子來講。 我們現在看的例子是: 可能 1 萬個人, 我們去調查他們的退休年齡, 然後你把那個樣本畫出來, 它的分布是這樣子, 看起來有像常態分布嗎? 沒有, 它左右不對稱, 沒有像那種鐘形曲線的常態分布, 所以這個資料並不是一個常態分布的資料。 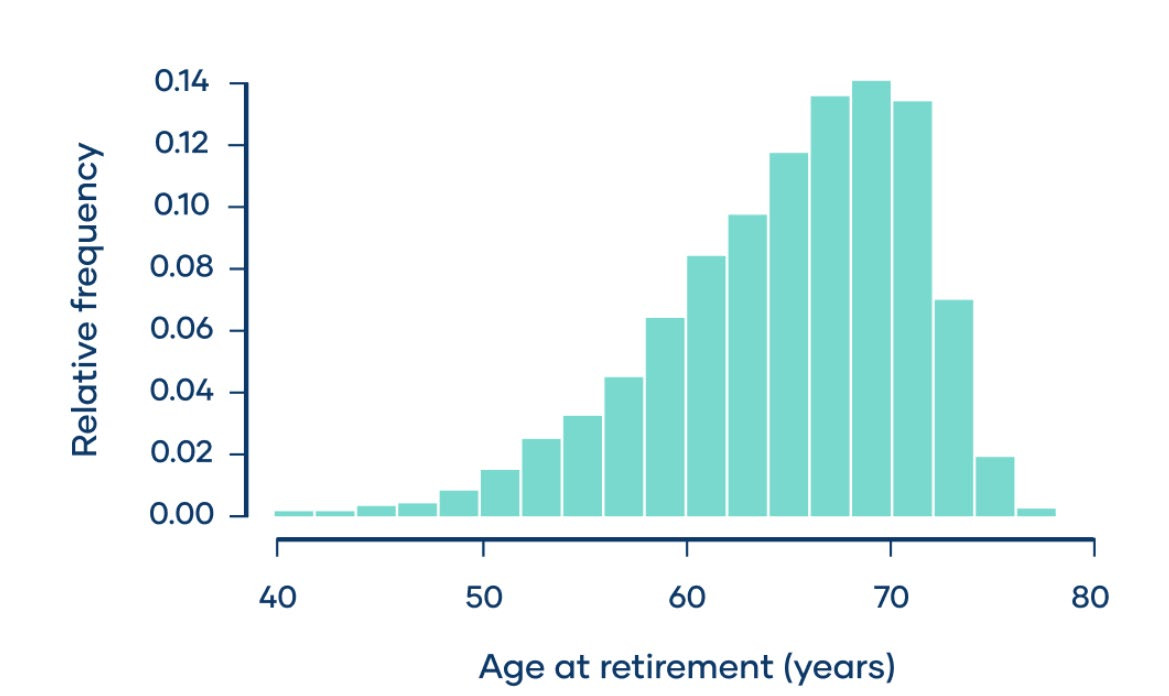 你也可以想, 例如說 1 萬個人把它分成 1 萬組, 一個人一組, 然後把每一組的平均值畫出來是這樣, 對不對? 我們現在也可以用另外一種呈現法: 1 萬人, 我們把它分成一千組, 10 人一組, 然後去畫那 10 人一組的平均值。 我們把那個一千的數字把它畫出來, 它長這樣就會像左圖這樣, 看起來就比較像常態分布, 是不是? 有像喔, 就是這樣圓圓的左右對稱。 你如果再分更多人一組, 例如說我把它分成 100 組每組 100 個人, 然後去取那個 100 個人的平均的退休年齡, 然後把 100 個數字畫出來, 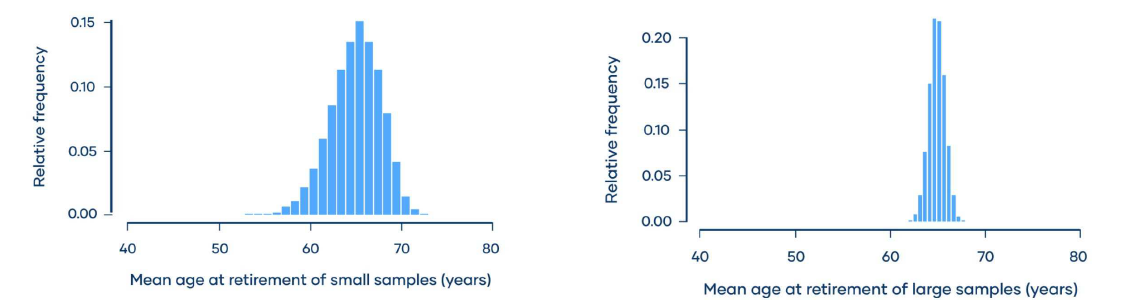 它長的就是右圖這樣, 看起來左右平均, 的確就是很像一個常態分布, 對不對? 這就是中央極限定理告訴你的第一件事情: 如果要取平均值的話, 樣本數越大取得的平均值, 就會越來越像常態分布。 第二件事情就是你比較左圖和右圖, 右圖是不是比較尖、 比較高? 左圖是不是比較肥? 我們剛剛講到變異數; 如果說平均的樣本的數量 $N$ 越高的話, 變異數就會越來越小, 變小的方式就是以 $\frac 1{\sqrt{N}}$ 來減少; 左圖 $N$ 是 100, 因為是 100 人一組, 右圖 $N$ 就是 10, 因為 10 人一組; 它就會越來越尖、 越來越小, 然後越來越像常態分布。 這和我們的世界有什麼關係? 比如說, 快到選舉的時候, 你們可能還不能投票, 但是可能家裡的大人都會一直在講: 民調現在幾%, 對不對? 一家的民調怎麼樣? 民調到底準不準? 我問你一個問題, 很簡單, 大家隨便猜一下, 反正不是在考試。 我想要知道台灣人對打疫苗的想法。 我做了四份民調, 或者是有四組人做了四份民調: 在中研院門口訪問 10 人、 全國隨機市話訪問 10 人、 在中研院門口訪問 500 人、 全國隨機市話訪問 500 人, 哪一組你覺得相對來講比較有參考價值? 看起來好像絕大多數的人, 都覺得相對來講有參考價值的是, 第一: 不是 10 人的, 是 500 人的樣本數, 第二: 不是今天在中研院門口訪問, 而是全國隨機實況訪問。 的確理論上來講, 這是比較好的, 比較值得參考的一份調查。 為什麼呢, 有兩個因素。 這就是告訴我們說, 民調會不準有兩個原因: 第一個是抽樣(隨機)的誤差; 我們剛剛那個中央極限定律, 告訴我們說, 隨著樣本數 $N$ 的增加, 抽樣的誤差, 會以 $\frac 1{\sqrt N}$ 來減少, 對不對? 那也就是像你丟骰子一樣, 例如說你丟 $N$ 次平均, 你丟出來的平均數和 3.5 的距離, 也是會以這樣子的定律來減少。 第二個叫做系統誤差; 這個問題就是: 樣本是不是有代表性? 你們可能有聽過, call in 的民調通常是完全不準, 為什麼? 因為它的抽樣很有可能沒有代表性, 只有會去看這個特定的 call in 的節目的人, 才會打電話進去, 對不對? 他可能有他自己的, 譬如說政黨偏好, 或者是生活習慣, 那麼就不足以代表, 是不是? 不具全國大家的代表性。 當然數學家沒有辦法幫你回答, 但這也就是為什麼我們每次到選舉都會有這種討論: 是不是市話民調比較準, 手機民調比較準? 要幾 %、 可以幾 % 這樣混合起來會準? 然後大家在那邊吵翻天, 吵的就是: 要怎麼樣去做這個調查, 樣本才會代表譬如說一個平均的台灣的樣子、 台灣選民。 基本上, 從你們剛剛已經聽到的, 譬如說, 中央極限定理或者是大數定理, 基本上就可以回答這個問題。 當初在參選的時候, 他們是不是有很多爭論: 什麼是誤差值? 到底是什麼讓 6% 或者讓 3%? 反正就是這些東西。 你用前面這些定理, 自己就可以分辨。 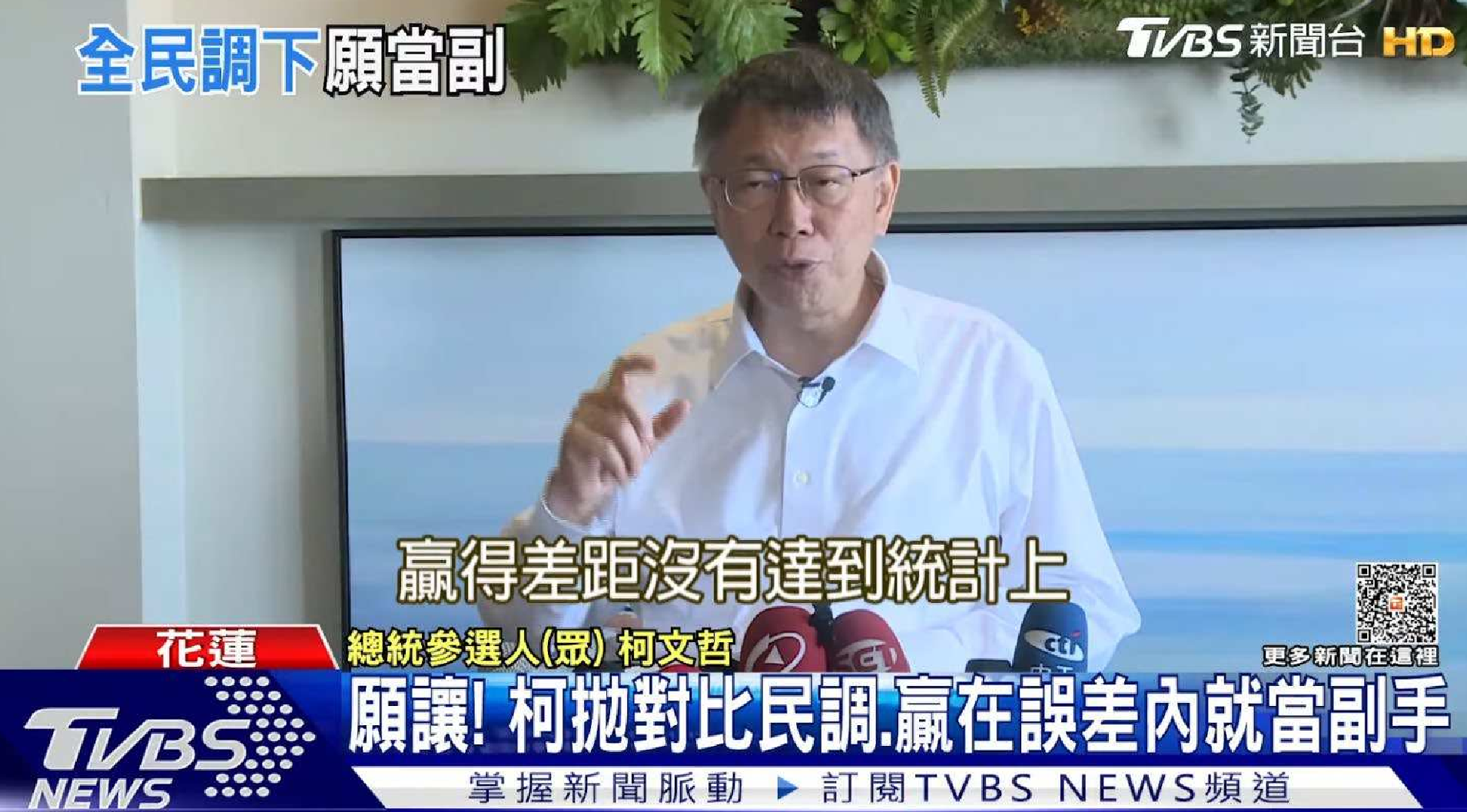 統計就講到這邊。 統計就是在做這些事情。 希望我已經說服你們: 懂一些統計, 真的對理解世界來講, 非常重要。 機率接下來在講的就是機率, 這和統計很相關。 機率在講什麼? 就是事情發生的機率。 譬如說, 我們來看看大家對機率的概念。 朋友今天傳一個簡訊來說: 我快篩陽性今天不出門。 我想知道的就是, 那準嗎? 結果這位朋友說這個快篩品質還不錯; 據檢驗, 如果真的有得新冠的話, 快篩出來兩條線的機率是 8 成, 沒有得的話, 測出來一條線的比率是 9 成, 這個快篩品質不錯。 現在疫情還在流行; 目前有得新冠的人, 大概是總人口數的 1%, 那麼你就可以算出來, 得新冠的機率是多少? 結果出來囉, 很多人覺得是 8 成以上, 最多人回答的是 5 成到 8 成比例。 正確答案是最少人選的嗎? 大家學一下機率, 我現在就算給你們看。 記得喔, 你想想看: 現在有 1% 的人得新冠, 對不對? 照這個比率, 得新冠的這些人快篩出來陽性的比率是 80%; 現在如果這些人全部都去做快篩的話, 0.8% 的人是真的有得。 相同的, 既然說 1% 的人得了新冠, 99% 的人目前沒得新冠, 對不對? 其中的 9 成出來是一條線, 其中的 1 成 9.9% 出來是兩條線。 那麼我們現在重點就是: 我已經知道這個朋友是在一個範圍裡面, 他測出兩條線對不對? 已知他測出兩條線, 然後在這前提之下, 他真的有得新冠的機率, 是不是 0.8 和 9.9 這兩個數加起來變成分母, 然後 0.8 變成分子? $\frac{0.8}{0.8+9.9}=\frac{0.8}{10.7}$, 機率只有 7.5%。 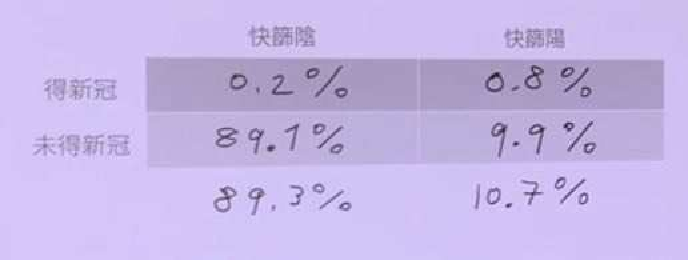 如果說今天新冠真的很流行, 10% 的人現在都得新冠, 我們就知道這個數字會怎麼改變;機率是會再上升, 對不對? 如果這個朋友又有跟你說, 除了兩條線之外, 他還喉嚨癢、 頭痛, 還有一點發燒, 那麼你就可能要再把那個表弄得更大, 就是有喉嚨癢、 頭痛又發燒的, 得新冠的機率是多少? 那麼你算出來這個機率也會變大很多。 這就是代表說機率是很重要的事情, 然後有時候和你想的真的不一樣; 還是要學一下、想一下, 把那個邏輯想一遍, 你對事情會有比較正確的判斷。 統計與機率, 我差不多就講到這裡。 順帶一提, 你如果對這有興趣的話, 這叫貝氏定理。我們中研院當然也有統計所, 所以我現在有點搶人家的事情來做。 但是基本上對於國中生、 高中生這樣子的年紀來講, 統計還是算在數學的一部分。 只是說因為統計真的很重要, 所以有一些專業研究機構會把統計單獨分出。 好, 大家有問題嗎?沒有的話, 我們就來回到比較是古典的數學, 那就從數數字開始。 就像我們從剛剛講的, 從小開始, 第一次接觸到數學, 可能不是除法、開根號, 可能是數數。  II. 數數數的話, 感覺是非常自然的事情, 甚至正整數是在巴比倫時代就發明了, 叫巴比倫數字系統, 所以是從五千年前之前就有這樣的數。 因為它很自然, 所以它就叫自然數。 到了十九世紀, 有一位非常著名的數學家 Kronecker, 對數學做出了很大的貢獻; 他說神創造了自然數, 其他都是人造的。  自然數有很多很棒的性質, 比如說自然數加自然數, 正整數加正整數, 還會是正整數, 正整數乘以正整數也還會是正整數。 所以你可能到小學三年級吧, 數學課都是很開心的, 只有在討論正整數而已。 我們剛剛有講到乘法, 那麼你可以開始問: 2 的倍數是什麼? 2、 22、 24、 236。 2 的倍數除了它自己以外的倍數。 我們把它用紅色劃掉。 同樣的 3 的倍數我們把它用橘色劃掉。 然後你可以這樣子再重複, 譬如說, 5 的倍數除了自己的把它劃掉, 7 的倍數除了它自己的把它劃掉, 沒劃掉的就繼續乘。 為什麼沒有 41? 蛤? 沒有塗到耶, 沒有劃到也沒有塗到耶; 好, 那請用在你自己腦子裡, 用你自己腦子的螢光筆, 去把 41 塗一下好不好。  剩下來的就是所謂的質數, 因為它沒有辦法被 1 和它自己之外的其他數除盡。 我們剛剛講的很笨的方式, 就是希臘數學家在兩千多年前尋找質數的方式。 我們現在科技很進步, 對不對?但是其實找質數的方式還是差不多。 好, 質數很酷, 它是正整數界的不可分割的原子, 其他的數就可以用質數去乘, 然後把它乘出來, 但是它自己沒有辦法如此。 但是它和世界有什麼關係呢? 現在就是講一個小故事。 質數其實在自然界裡面常常出現。 我就舉一個例子, 因為今年剛好是一個很適合講這個的年。 自然界裡面有很多奇奇怪怪的生物, 有一種叫週期蟬, 它的一生基本上都是在地下, 是地下蟲生。 小 baby 生出來之後就鑽到地下了。 在那裡 $N$ 年之後的夏天才會破土而出, 然後在四個禮拜之內羽化、 交配、 產卵, 做一些傳宗接代的事情, 然後它就化了。 它的卵孵出來之後, baby 又爬到地下裡面。 以我們的角度來講這是蠻悲慘的蟲生。 現在問題是: 它的週期 $N$ 到底是多大? 大家都有聽過, 很酷, 對。 在北美, 主要在美國, 有兩種週期蟬, 一種的週期是 13, 一種是 17, 好巧都是質數; 它是真的只是一個巧合嗎? 不管, 反正 13 或 17 年。 那麼要幾年這兩種蟲才會相遇呢? 221。 因為它兩個都質數, 所以你要把 13 和 17 乘起來就 221。 今年的夏天, 這兩種蟬就同時出現在北美; 有上兆隻, 聽說超級噁心。  221年才會一遇;這對它們來講, 有什麼意義呢? 我們是不是可以相信說, 是因為演化的選擇, 才讓它們都是質數呢? 因為兩種蟬相遇, 對它們是好事還是壞事? 壞事, 因為它們要搶食物, 要搶資源, 要搶地, 對不對? 你看這個好可怕, 甚至還會有雜交的問題。 譬如說假如說一個周期12年, 一個周期 15 年, 它們 60 年就遇一次, 可能這樣遇幾次的時候就絕種了。 所以物競天擇剩下來的, 可能就是質數周期的。 質數常常以這樣子的方式出現在自然界。 不只自然界, 我們待會再講, 質數其實非常地難處理。 例如說, 19 世紀的 Lucas 花了很多很多時間, 在 1876 年證明這個數 $2^{67}-1 =147,573,952,589,676,412,927 =$ 一百萬兆 $\cdots\cdots$, 21 位, 不是質數。 但是你要證明它不是質數, 就是很想要把它做質數分解, 找出來到底是什麼數乘什麼數乘什麼數才會變成它。 這其實是一件非常難處理的事情, 即使現在電腦很厲害、 很厲害, 這還是很難解的事情。 有位 Cole 先生花了很多很多年, 據說每個禮拜天都在做這件事情; 禮拜天要陪小孩玩會怎樣?為什麼數學家要那麼無聊? 喔, 這你就不懂嘛, 這個解出來很開心啊, 而且你就是很想知道, 晚上就一直在想這件事情;可是要上班, 沒關係, 我禮拜天再來做一次運算好了。 可能就是這樣子, 而且他不是唯一一個人。 1903 年他解出來之後, 據說給了一場非常轟動的演講。 他一整個演講不像我一直囉哩巴唆, 他一句話都沒有講。 他走到黑板前面, 左邊寫這個方程式 $2^{67}-1 =147,573,952,589,676,412,927$, 然後他走到黑板的右邊, 寫了 $193,707,721 \times 761,838,257,287$, 然後他就開始算, 算了一個小時, 寫得密密麻麻, 最後得到這個數 147,573,952,589,676,412,927, 丟了成品就走了。 然後大家就站起來, 幫他拍手。 所以不是他一個人而已喔, 大家都覺得: 你好帥帥, 算得出來實在是太棒。 所以還是有很多人, 不覺得這個無聊。 數學對我們、 對現在的社會, 或者科技是多麼的重要。 你如果去讀數學史的話, 就知道這些其實是很多很多無聊的人一點一滴建造出來。 質數分解實在是太難了, 沒有他們這麼無聊, 可能你今天就沒有辦法網購了。 在網路上買一大堆有的沒的, 永遠都不會用到的東西, 都要感謝這些人, 為什麼呢? 網購時是不是要輸入你的信用卡號碼? 你有想要每個人都知道你的信用卡號碼嗎? 你只想要商家知道, 對不對? 商家譬如說, 蝦皮、 亞馬遜, 不曉得, 他們怎麼知道呢? 它的處理方式是這樣子的。 我把一個很大很大的質數 $p$, 再乘以另外一個很大很大的質數 $q$, 然後得到一個爆炸大的自然數, 我們叫它 $m$, 現在大家用的大概是 50 位這麼多。 質數 $p$ 和 $q$ 只有我知道, 然後我不跟你說。 但是我跟你說什麼? 我跟你說這個乘起來的結果 $m$; 大家都可以看得到它; 沒關係的, 都給你看, 因為就算知道這個數, 你也沒有辦法把 $p$ 和 $q$ 找出來, 對不對? 才 21 位的數, 那位老兄就花了幾年的禮拜天計算, 對不對? 現在這 50 位的數, 沒有人也沒有電腦可以在很快的時間裡面解出來。 所以我就很大方地跟你講。 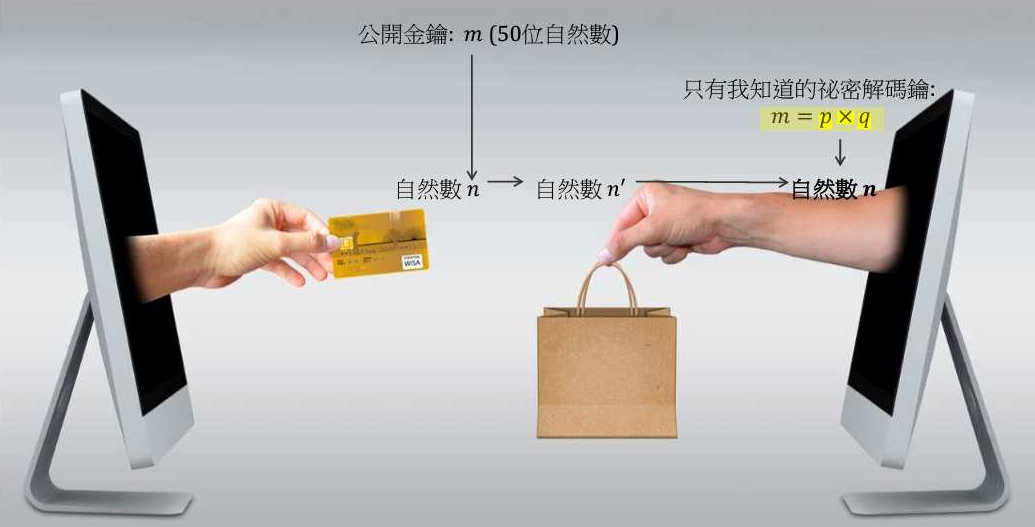 然後我就在網購時輸入我的信用卡號碼。 電腦系統就把這個信用卡號碼變成另外一個正整數 $n$。 它就可以用這個公開的、 很大的數 $n$, 得出另外一個正整數 $n'$; 細節我就不講, 有一點點複雜。 這個正整數 $n'$ 我就傳給你囉。問題就是在這個箭號 $n'\to n$; 如果我可以把這個箭號反過來、 推回去的話, 我就可以知道這個信用卡號碼是什麼。 問題是說我要把這個箭號反推回去的話, 我需要的是什麼?我需要的是 $p$ 和 $q$。 我不知道這個很大的數的質數分解的話, 就沒有辦法把這個箭號反回去。 所以不管淘寶、 亞馬遜, 就靠著這個 $p$ 跟 $q$, 把那個箭號又反推回去, 來知道你的信用卡號碼。 這就是現在我們每天要用到質數的一個方法。 所以不要嫌我們數學家無聊喔。 質數這麼酷這麼有用, 我們是不是想要知道: 總共有幾個質數? 還是你們覺得只有一兩位數學家想要知道這個, 但是其實從希臘那時候就很多數學家想要知道這個問題, 而且把解答解出來了, 還證明給你看。 其實很簡單。 例如說我假設我數學真的很爛, 我就猜想說: 世界上只有 2、 3、 5, 三個質數而已, 我就把這三個數乘起來變成 30, 然後再加上 1, 得到另外一個正整數 31。 結果我算了半天什麼數可以除盡 31, 沒有耶, 哇, 31 也是質數, 所以我的假設錯了, 並不是只有這三個質數; 好, 那我們現在要認錯。 我們現在開始假設, 現在有四個質數。 假如只有 2, 3, 5, 31 四個質數。 考慮 $X=2\times 3\times 5\times 31+1=931$。 但是檢查發現 $931=7\times 19$ 不是質數。 所以不是只有 2, 3, 5, 31 四個質數, 還有 7 和 19。 所以說我的假設還是錯的。 我就一直重複下去囉, 對不對? 這個重點就是說, 你如果把幾個質數乘起來再加上 1, 因為 1 沒有辦法被任何其他數除盡, 所以這個數沒有辦法被這些質數裡面任何一個除盡。 你可以想像這個循環一直無限輪迴下去。 如果你有這樣子的想法的話, 你就可以證明。 歐幾里得在很早之前(300 BC)就證明: 有無限多個質數。 他的方法就是: 假設我覺得有 $N$ 個質數 $p_1,p_2,\ldots,p_N$, 然後我把它全部乘起來再加上 1, 得到 $X=p_1\cdot p_2\cdots p_{N}+1$ 那麼就只有兩種情況: 情況一是: $X$ 是質數, 那我假設就錯了, 我要再多得到一個質數。 情況二是: $X$ 不是質數, 那麼它一定可以被其他的數除盡; 而且我們剛剛講過, 因為 1 不能被任何數除盡, 所以 $X$ 一定不是被這幾個質數 $p_1,p_2,\ldots ,p_N$ 除盡, 所以我們又發現了其他的質數。 所以以上任何的情況, 都跟假設相矛盾, 這樣子我們一定會有無限多個質數。 那麼我問你喔, 你們猜一猜, 如果一直重複這樣子的輪迴, 當然不要有錯誤啦, 所有的質數都可以被這樣找出來嗎? 猜一猜, 我不知道那個時候你幾歲; 假設你可以永遠活著, 任何一個質數都可以這樣被找出來嗎? 你們想知道答案嗎? 答案是: 數學家到今天還不知道。 大家這個問題, 幾千年來很多人去研究, 還沒有一個定論, 所以就靠你們了。 而且質數真的是很奇怪, 因為它雖然那麼簡單, 但是到現在, 數學界很多很有名的大難題, 還是關於質數的性質。 例如說, 很有名的 Goldbach 猜想, 它其實就是很簡單, 猜想每一個偶數都是兩個質數加起來, 我們到現在還是沒有辦法去證明它是對還是不對。 而且更奇怪, 例如說, 十九世紀有位數學家叫做 Mertens, 為了研究質數的性質, 定義了一個 Mertens 函數, 對每一個正整數 $n$, 都得出另外一個數 $m(n)$, 然後他的猜想就是說: 每一個自然數的 Mertens 函數值 $m(n)$ 都會小於一。 然後大家就很努力, 到了九零年代, 數學家已經檢查了幾萬兆的自然數, Mertens 猜想都是對的。 你去檢查 1、 2、 3、 4、 5, 人家覺得你怎麼這麼無聊, 那麼人家檢查上萬兆的就一定是對的嗎? 居然不是, 居然就是被人家證明出來其實這猜想是錯的。 但是我們大家還是找不出來, 到底哪一個數是錯的。 所以就是會有這種很奇怪的事情。 質數真的是一個非常奇怪的東西, 大家以後如果想要當數學家的話, 可能也會被質數吸引到。 證明的必要性這也就告訴我們, 為什麼數學家要證明。 有時候覺得證明很慢, 因為其他不用證明的科學, 都可以一個對、 兩個對, 就差不多對了, 我們就接下來做下一步。 但是數學不是這樣, 你一定要一直去證明。 第一:證明是帶來數學的自由, 譬如說像歐幾里德對質數的證明; 雖然我們找不出那些質數, 但是還是可以用很抽象的方法, 證明出來說: 不用猜了啦, 就無限多個, 數也數不完, 這就代表他的自由。 證明給我們這個自由。 可能人在有限的生命裡面, 沒有辦法去計算某些事情, 但是還是可以得到非常準確的知識。  第二:證明帶來數學的真實。 就是像剛剛講的 Mertens 猜想, 是一個正確了一萬兆次的事情, 但是還是可能是錯的。 所以沒有證明, 你做的數學就是很像用沙堆塔一樣。 如果數學像是蓋城堡, 你要一個證明; 已經證明過的事實你才可以放上去, 這樣子就不會倒。 大家如果學到證明了, 就不要覺得很煩, 還是有用的。 III. 當自然數不敷使用講那麼多都是關於自然數。 除了自然數以外, 還有什麼? 因為很有趣的事情是, 巴比倫時代, 數學非常好, 但是他們的數字裡面沒有 0。 現在對你們很自然的, 例如說 0 的概念, 其實是數學家花了幾千年才慢慢建立起來的概念, 結果你們小學就全部學到了。 我們剛剛講說, 正整數加正整數是正整數, 相乘也是得到正整數, 但是減咧? 你如果想要問: 我欠你多少? 例如說, 昨天借我 20, 我今天花你 10 萬, 那麼我還欠你多少? 那麼就是要負數。 這個負數 2000 多年之後才出現, 300BC 時首次出現於《九章算經》。 據我們所知, 那個減法的概念, 真的是要等; 譬如說農業社會非常成熟之後, 人才會開始處理這個概念。  接下來處理的, 是正整數除以正整數, 它不一定是正整數。 我們小時候碰到除法的時候, 一開始說, 喔, 除不盡, 除不盡就不管了, 然後講餘數什麼。 你要長大一點才會教你, 其實有分數這種東西。 但是我們從小就知道, 切蛋糕切披薩, 我要一塊我要一塊, 大家都要平分, 那個其實就是分數的開始。  分數再加上整數, 形成所有有理數。 一個很神奇的事情發生了: 從 0 到 1 之間, 有幾個有理數? 無限多個, 對不對? 從 0 到 1, 你永遠都可以中間取一半, 然後再取一半, 然後再取一半, 無限地做下去, 到最後就越來越密; 所以在有限的範圍裡面, 有無限多個數。 那就是有理數很奇怪的地方。 例如說, $\pi$ 圓周長, 我們大概都知道, 它不是一個分數, 它不是一個有理數, 但是我們可以寫五十位的數, 它都還是一個有理數。 在實際生活, 我們一直可以都用有理數去逼近任何一個數, 用的就是這個性質。 再說一個生活上的例子。 例如說, 我們都會講說, 2 月 29 日生日的人很倒楣, 四年才過一次生日, 為什麼? 因為一年就是我們轉了個週期, 大概有 365.242191$\cdots$ 這麼多天, 對不對? 它不是整數啊, 那該怎麼辦? 可是我們做月曆總是要有整數嘛。 最簡單的方式就是, 每四年有閏年, 閏年的時候就會多一天, 就塞一天進去, 那麼你平均下來, 一年就有 365.25 天, 這就和 $365.242191\cdots$ 比較像, 但每一百年還是會有一天的誤差。 波斯曆就算得更準, 每 33 年有 8 個閏年, 這就把後面那些小數點用 8/33 去代替, 它算的是不是就更準了? 這樣子差不多一千年的誤差還不到一天而已。 羅馬教皇的 Gregorian 曆, 是我們現在在用的, 就算得更精準了, 400 年有 97 年的閏年。 你可以用越來越複雜的月曆, 讓天數越來越準。 這個數字明明就不是有理數, 但是你可以用有理數做曆法。 那很棒啊。 我們就想說: 有理數就夠了嗎? 還有沒有其他的?  在希臘的時候, 就有人偷偷發現有理數還不夠。因為畢達德哥拉斯定理告訴我們直角三角形的邊長的關係, 我們就知道:這最長的邊是 $\sqrt 2$。 問題是 $\sqrt 2$ 是有理數嗎? 這個事情很嚴重, 據說證明這件事的人被丟進海裡, 很慘, 因為 $\sqrt 2$ 不是有理數這件事情, 實在是太讓人震驚。 現在可以來看一下影片休息一下, 裡面用了一個非常簡單的方法去證明 $\sqrt 2$ 不是有理數, 十秒鐘的歌就證完了。  重點是它改變了人類對數字的想像: 居然有理數還是不夠的。 其他不是有理數的數, 我們要叫什麼呢? 就是無理數嘛。 這兩者合起來我們就叫它實數。 你可以拉一條線, 在線上的所有數都叫做實數。 這樣夠複雜了吧。 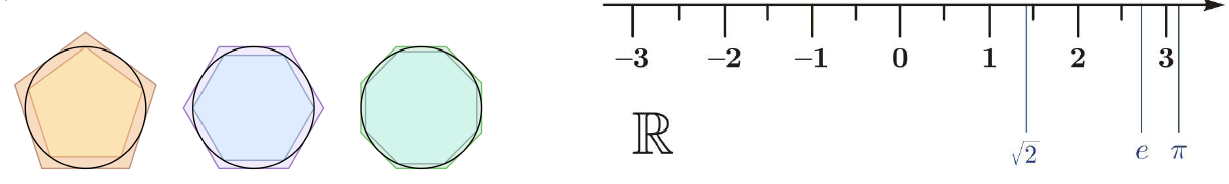 問題是說, 我們剛剛發現了實數, 是因為我們拿2去開根號對不對, 那麼我們能不能拿其他實數去開根號? 可以啊, 為什麼不可以? 可是問題是, 我如果拿 $-1$ 去開根號, 怎麼辦? 那不對嘛, 你拿正的數也不對啊, 因為正正得正啊, 你拿負的數也不對啊, 又負負得正啊, 所以就沒有實數可以是 $-1$ 的開根號, 那可怎麼辦呢? 就只好自己再發明新的東西啊。 所以我們就發明了一個叫做 $i$ 的東西, $i$ 是什麼? 你問我 $i$ 是什麼, $i$ 就是 $-1$ 的開根號啊, 不過那到底是什麼? 那就是 $i$ 啊, 這就是數學上的定義。 我沒有要再去解釋, 它就是這樣, 數學家說的, 好, 那我們就這樣定義啊。 那是不是越來越麻煩? 所以說, 除了實數之外, 我們又有這些叫做虛數, 因為它不實嘛, 不實的數叫 $i$。 我既然發明了一個 $i$ , 我就可以去發明「半個 $i$」, 然後再去發明「負 0.5 的 $i$」, 對不對? 那這件事情就越來越麻煩了, 對不對? 這就是虛數。 更麻煩的是, 我是不是可以把實數和虛數加起來? 我是數學家, 我說可以就可以; 好, 出來那些數, 就叫做複數, 因為它很複雜。 那麼為什麼要這樣自我折磨呢? 好, 我們來看一下, 這就講到代數。 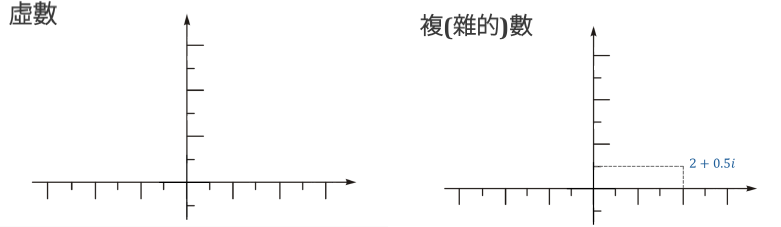 我們剛剛為什麼要把 $-1$ 去拿去開根號? 因為我可能很想去解這個數學方程 $x^2+1=0$, 是吧? 而且, 這個學校都要學啊, 對不對? 學校需要學, 我只好學啊, 學怎麼解方程式 $ax^2+bx+c=0$, $a ,b,c$ 可以是任何數; 我就取 $a$ 是 $1, b$ 是 $0, c$ 是 1。 問題是說, 你有沒有想過說: 我為什麼要學這個東西? 和我到底有什麼關係? 大部分的人都學過這個東西, 那麼學這個到底要幹嘛? 代數學代數到底要幹嘛? 在希臘時代大家多開心, 做尺規作圖就好了嘛, 對不對? 不但在希臘, 像在漢朝出土的一些漢朝文物上面, 都有伏羲跟女媧, 就是一個規一個矩, 就是尺規做的。 以後是不是不要罵人家沒規矩, 只要罵人家沒代數。    尺規可以做出這些圖, 都可以用二次方程式來描述, 那很好啊, 代表說尺規作圖可以去取代二次方程式。 那麼我為什麼還要有更多的東西呢? 尺規作圖沒有辦法解決所有的問題, 例如說, 大家都有學過尺規作圖二等分角。 因為希臘人真的很喜歡尺規作圖, 他們就開始問超級大難題: 要怎麼用尺規作圖去三等分角? 昨天我有上網去找一下, 真的有 YouTube 影片教你怎麼三等分角, 然後還上萬個人看過。 這就是告訴我們說, 網上的東西看看就好; 因為這早就被人家證明出來: 尺規作圖不可能做出三等分角。 證明的方式大概就是說: 用尺規作圖做出三等分角, 等同於說: 你要去用尺規作圖去解這個三次方程式 $y^2=ax^3+bx^2+cx+d$。 同時我們數學家早就證明: 只有一次及二次方程式的解可以用尺規做。 你們可以自己去找一找那個 YouTube 影片來看看, 然後看看就好。 代數帶來自由我現在想要告訴你們, 代數其實真的是很有用, 因為代數給我們的是自由; 這是什麼意思? 例如說二次方程式 $x^2+y^2=1$ 有兩個變數, 我可以畫出紙上的一個圓, 對不對? 如果我們再加一個變數, 它是一個球。 可是如果我們不依賴圖像, 而依賴代數的話, 就不一定要二維和三維而已, 我們要幾維都可以。 即使畫不出來的東西, 數學家還是可以處理, 因為有代數。 這就是我講的自由。 代數讓我們可以研究畫不出來的高維物體。 問題是你們想說: 我好好的, 要去研究 120 維的球, 我是幹嘛? 就像那位同學講的說, 數學家為什麼要那麼無聊? 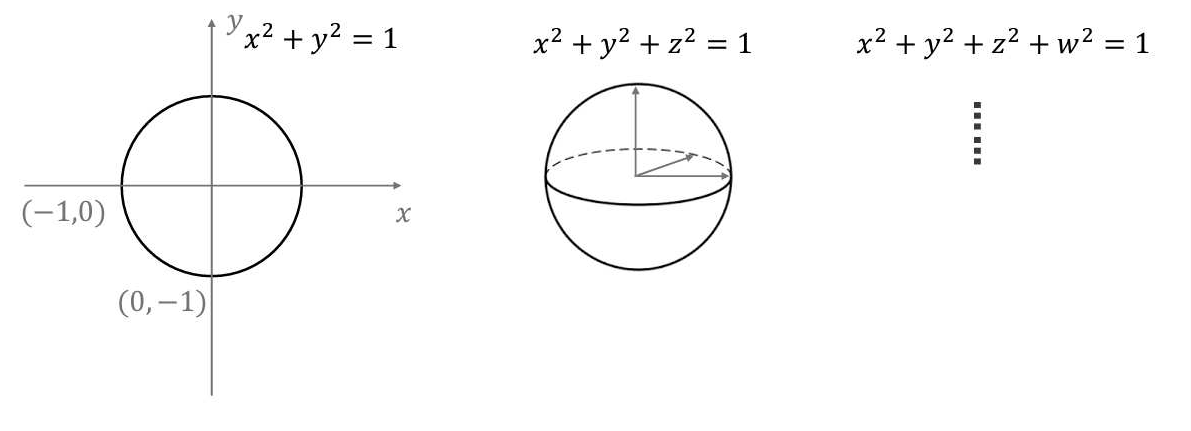  我現在就給你幾個例子, 你的生活中一直在運用高維體的物體的數學。 第一個可能比較抽象。 有些東西, 你在低維度看, 看得很模糊, 在高維就很清楚。 例如說我們剛剛講的這些曲線、 拋物線、 圓圈、 橢圓這些, 看起來都很不一樣, 但你如果由一個三維的角度來看, 它其實是同一個物體的不同切面; 它就是圓錐切面, 只是切的角度不一樣, 就可以切出不一樣的曲線。 這個例子很多, 譬如說, 不沾鍋的原理, 其實也是可以用這樣去理解, 這個沒時間講, 就算了。 所以說, 高維度的自由可以讓我們帶來更多的理解。 而且高維度空間無所不在。 譬如說, 一張圖好了。大家都很喜歡照相, 這張圖在你的晶片裡都到底是怎麼處理?這張圖處理的方式是, 把它變成一個在三千多維度的一個點, 為什麼? 有想過嗎? 我特別找了一個解析度很低的, $32 \times 32$ 而已, 它的每一個像素都有三個實數, 代表紅、 綠、 藍, 三色的訊號強度。 例如說像這個, 就是紅比較強。所以每一個像素都是一個三維空間裡面的點。 你總共有 $32 \times 32$ 這麼多像素, 所以你算出來, 這張圖是 $32 \times 32 \times 3(=3072)$ 三千多維的空間裡面的一個點。 它在我們的電腦裡面就是這樣處理。 你們平常很好的手機照起來, 都是上百萬維度的空間在做運算。所以說:沒有代數的概念, 光靠尺規作圖, 難怪希臘人沒有濾鏡, 更別提說現在走紅的人工智慧。  數字會被數學家搞得越來越複雜?我們就講一講, 是不是單純數字被數學家搞得越來越複雜? 從一開始, 大概五千年前, 我們數數, 很自然的自然數。 再過了兩千年, 出現負數和零; 零是一個人類非常重要的發明。自然數再加上零及負的整數, 我們就有了整數。 因為我們要考慮除法, 所以小學我們就學過有理數、分數, 對不對? 可是, 比如說, 有畢達哥拉斯的定理, 所以我們就想要開個根號, 結果發現又不夠用, 實數又要進來了, 越來越大。 我就覺得說, 自然數可以加根號, 其他整數我也要開根號, 就變複數了。所以會越來越大 越來越複雜。 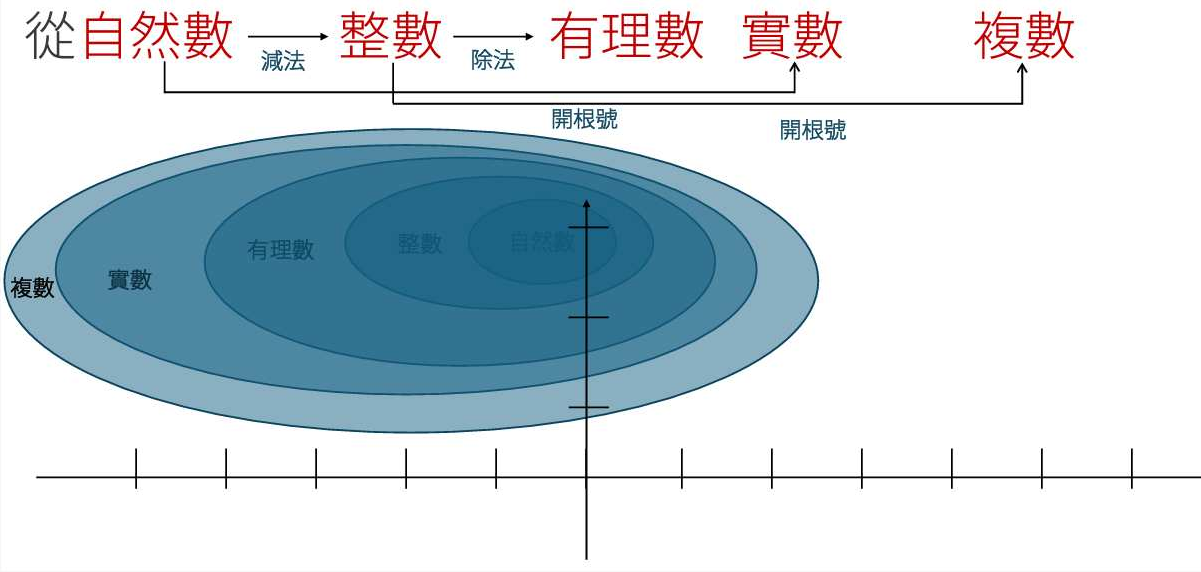  那麼為什麼我要停在開根號? 我們講過啦, 代數啊, 我可以有無限維度, 我可以有三次方程式, 那麼為什麼我要停在這裡, 是數學家累了嗎? 你們覺得呢? 其實不是。 其實據說發明微積分的萊布尼茨, 也覺得要發明新的數才可以解這個方程式 $X^4=-1$, 結果他錯了, 因為你可以證明: 其實複數就可以解那個方程式。 我這邊計算給你看: $X=\pm \frac{\sqrt 2}2\pm \frac{\sqrt 2}2 i$。 反正細節不重要, 自己去算一算, 就會發現它的四次方就是 $-1$。 而且你也可以證明: 其實複數就足以解答所有多項方程式 $a_n x^n+\cdots+a_1 x+a_0=0$。 所以數學還是蠻仁慈的, 我們不會要一直去發明新的數, 不然的話學不完。 所以我就問你, 沒有對錯, 只是問你的意見。 我現在跟你講這個故事後, 你還是覺得說, 只有自然數是自然的, 其他都數學家找出來折磨人的嗎? IV. 生活中的無限阿基里斯賽烏龜無限又是另外一個感覺非常人工的概念。 這個故事有看過嗎? 有些人有看過, 就是跑得很快的阿基里斯和烏龜賽跑。 他說: 烏龜, 你跑得這麼慢, 我跑的是你的十倍速, 所以我隨便讓你的十公尺。 然後烏龜說: 真的嗎, 你覺得你會贏嗎? 阿基里斯跑了十公尺之後, 烏龜只跑了一公尺。 在這裡, 阿基里斯從落後十公尺, 變成落後一公尺。 然後他說: 一公尺我下一次就追到。他就追到這裡, 結果烏龜領先了 0.1 公尺, 然後他追到這裡; 烏龜領先了越來越少, 可是好像還是一直有領先;對, 沒錯, 就是多走我一步。 但是他的邏輯到底錯在哪裡呢? 你們應該不會有人真的覺得烏龜永遠會贏, 不可能啊。  為什麼希臘人一直卡在這裡? 這到底什麼一回事呢? 就是因為要怎麼處理無限小、 無限大、 無限多的概念, 在那時候還不成熟。 因為依照前面的算法, 當然這個有很多算法, 但是依照他的邏輯來講, 阿基里斯要超越烏龜, 他跑的公尺數要超過烏龜的, 對不對? 他要一直追, 追無限多次就追到了。 我們就把它加起來叫做 $x$。他的謬誤叫做 Zeno's 悖論。 Zeno's 悖論的謬誤就是說: 你有無限多個加號, 並不代表說答案是無限大。 有人知道這個要怎麼算嗎? 容易的算法就是: 我把它乘以 10; 乘以 10 的話, 這個 10 變 100, 1 變 10, 對不對? 可是它還是有無限多項。 然後把這兩個相減, 這些都 cancel 掉, 因為它們都是一樣, 所以我就得到說: 9 個 $x$ 是 100, 對不對? 所以 $x$ 是 $100/9$, 那是不是無限? 沒有, 很有限, 對不對? 他就是 100/9。 例如說我們現在的紀錄保持人, Usain Bolt, 這對他來講, 一秒就跑完了, 對不對? 他真的跑很快。   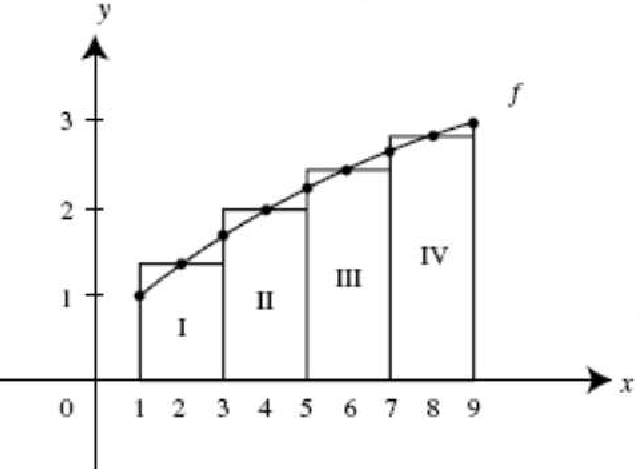 所以呢, 要處理這樣子的悖論, 我們要能夠去處理無限小、 無限大、 無限多的概念。 這還是要回到數學家。 或者是說, 我們要算例如說, 圓的周長, 或者是面積, 要怎麼算? 以前希臘人阿基米德把這個放在他的墓碑上面, 據說喔, 因為他覺得這實在是在當年最酷的方程式, 就是這個原柱體和這個圓球面積是一樣, 他怎麼算? 他也是把球面割得很小很小、 無限小的方格去算, 對不對? 現在我們把這個東西系統化, 叫做積分。  積分的概念其實也非常簡單, 我們有一個曲線, 想要算它下面的面積; 就像說這個曲線可能是一個圓, 我們就把它切成無限多條長方形去估計, 得到的這些無限多的、 無限細的長方形面積加起來, 就是它的真實面積。 這就是積分在做的事情。 其實這和之前阿基米德那些, 用的都是無限小這個概念, 所以這概念聽起來很人工, 但是他處理的卻是很自然的事情, 例如圓的面積。 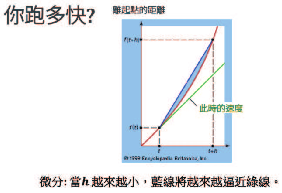 或者是說, 你要說我跑多快? 例如說, 我畫一個函數好了, 這個紅線是說我幾秒的時候跑了幾公尺。 因為我很厲害, 我要去比奧運, 所以我必須要非常精確地知道, 我每一個時間的精確地速度。 我現在有這個曲線, 要怎麼去算?例如說這個藍線, 它算的是什麼? 這個藍線在算的是說: 我在 $t$ 到 $t+h$ 這段時間的平均速度, 它就是這條藍線的斜率。 那麼我要怎麼去算? 我覺得讓 $h$ 變得越來越小, 越來越小, 這個藍線就會越來越像綠線。 因為綠線是切線, 綠線的斜率就是當下的速度。 這就是現代的微分, 與積分加起來就是微積分。 我們知道說, 沒有微積分, 其實現在任何的科技都不可能, 因為我們隨時都要知道而且很能夠很精確地算得出來, 例如說火箭的速度, 或者是面積有多少, 甚至說現在公司要做財報, 也都是要用到微積分。 這就是生活中的無限。 其實你就覺得有些事情聽起來, 是數學家又在無聊了, 但是其實並不是這樣。  V. 數學的美感最後幾分鐘, 我們就講了一些非常輕鬆的事情。數學不但很有用, 很有實用價值, 也是一個很有美感的東西, 或者是說, 很多美感也是要建構在數學之上。 那聽起來有點奇怪。 第一個我們要講的就是, 你可以同意也可以不同意, 這當然是見仁見智, 但是很多數學家會有這樣子的感覺, 就例如說我和同事、 其他數學家討論, 常常大家講說: 這篇文章很美, 那個方程式實在是太美了, 那講的到底是什麼? 那我覺得羅素他講得很好: 數學, 正確看待時, 不僅具有真理, 還具有至高的美, 一種冷而嚴峻的美, 一種屹立不搖的美, 如雕塑一般, 一種不為我們軟弱天性所動搖的美。 也不像繪畫或音樂有富麗堂皇的裝飾, 而是純粹地崇高、絕對地完美, 是最偉大的藝術, 然而這是極其純淨的美, 只有這個最偉大的藝術才能顯示出最冷酷的完美 (stern perfection)。[羅素 1918] 他形容一種冷而嚴峻的美, 一種屹立不搖的美。 為什麼是屹立不搖? 就像我剛剛說的, 就是數學是建立在證明上面;當然不是完全, 但是和其他的學科比起來, 因為它有證明, 證明當做基本, 所以它在這個基本上, 是會讓人有屹立不搖的感覺。那麼為什麼是冷而嚴峻呢?可能就是因為它很難, 老實說並不容易;可能你要一個結果; 可能要花很多很多的時間, 所以在當你自己在做的時候, 可能會有一種「這個方程式怎麼對我這麼差、這麼嚴厲, 可是又很美」這樣子的感覺, 其實就是很抽象的來講, 數學家常在追求一種完美的感覺。 音樂與數學我們再來看一些其他比較不很抽象的事情, 比如說數學和音樂。 你要去討論音樂, 其實也需要數學。像現在很多音樂可能是用合成器, 那裡面用到的也都是數學。 比如說中央C好了, 其實如果音叉打開來, 它的音波差不多就是長這樣, 左右軸是時間, 上下軸是它的訊號的大小。 它有一個固定的頻率, 像中央C差不多是 262 赫茲, 我們就把這個赫茲, 比如說叫做 $\omega$。 我如果今天把那個頻率變兩倍, 出來的是什麼音? 高八度的音, 大家都很有概念。 那我再問你, 有沒有人知道, 如果把中央 $C$ 的頻率乘三倍變成了什麼音? 猜得出來嗎? 有人猜出來嗎? 更高的 $C$? 錯。   為什麼? 因為其實每高八度, 頻率就要乘以二, 所以你要再高。 樂理上說 perfect five, 就是 $C$ 跟 $G$ 聽起來很和諧, 因為它的頻率也是剛好是三倍, 所以這個頻率其實出來的是 $G$。 在網路上有一些工具, 你可以唱歌, 然後它就把你的頻率弄出來, 用影像畫出來。 所以學樂理的時候, 可以順便學數學。 當然很多人就會去討論音樂和數學的關係。 除了這個之外, 有很多人分析的, 就是巴哈的賦格;他的布蘭登堡裡面很多對稱性, 是可以用數學去理解: 為什麼聽起來這麼和諧這麼好聽?就是因為它有一個數學的規律性在, 這個今天就不講。 黃金比例再講一個很數學的美感。這應該學校有學過, 就是黃金比例。 自然界裡面很多東西, 尤其是我們會覺得漂亮的東西, 都是黃金比例。 為什麼黃金比例會漂亮呢? 我覺得是因為它有一個自我相似的性質; 這樣子一個黃金比例的曲線, 可以一直一直畫下去, 每一個看起來都差不多。 你要算它最後的比率的話, 就這樣做: 大的長方形的比率例如說是 1 比 $x$, 對, 左邊長是 1; 小一點的長方形, 它的寬只剩 $x-1$, 對不對? 它的長是 1, 對不對? 但是我們要求這兩個長方形基本上形狀一模一樣, 大小的縮放而已, 比例是一模一樣。 這樣你得到一個二次方程式 $\frac x1=\frac 1{x-1}$, 就是 $x(x-1)=1$, 也就是 $x^2-x-1=0$。 你用大部分的人好像都還記得的方法去解, 就得出黃金比例 $x=\frac{1+\sqrt 5}2=1.618\cdots$, 對不對? 所以它美在哪裡, 也是要靠數學來理解。 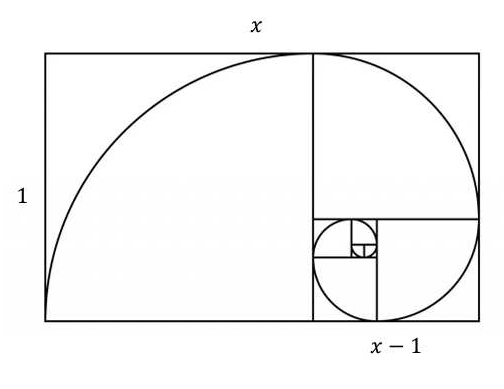  曼德柏(Mandelbrot)集合我今天講得差不多了。給你們看這個數學上出來的圖, 它美在哪裡?就是美在它的數學真的非常簡單。就是這樣子的一個無限循環的方程式 $z_{n+1}=z_n^2+c$。 就是給一個數 $z$, 這裡 $z$ 是我們剛剛講的複數, 所以才會是一個二維的圖;然後你把它平方, 然後再加上一個數 $c$, 然後你就得到下一個數, 而後你再去無限循環。 有些複數 $c$, 它的無限輪迴會是在一個範圍裡面轉, 那些數 $c$ 我們就劃黑的; 有些數 $c$ 會轉出去, 然後跑越來越遠、 越來越遠、 越來越遠, 那些數 $c$ 我們就把它上顏色; 跑越來越快, 越快的顏色就越淺。 然後我們就得到所謂的 Mandelbrot 的集合。 可是為什麼大家很知道這個問題? 就是因為這實在太漂亮了。 我演講就到這邊結束。 給你們看影片: 它一直放大, 可以無窮地放大下去。 如果禮拜天、下雨天沒事做, 把它打開, 就可以一直看。 看一下!快多多享受迷人數學吧, 真的是很多很漂亮的東西可以看。  本文作者任職中央研究院數學研究所 |
| 頁碼 | 35-52 |
2024年12月 48卷4期
以數學理解世界

