| 發刊日期 |
2025年6月
|
|---|---|
| 標題 | $n$ 次反三角函數之不定積分 |
| 作者 | |
| 關鍵字 | |
| 檔案下載 | |
| 全文 |
壹、前言筆者在查閲不定積分表時曾看到許多關於反三角函數的不定積分表達式, 但多為 1 次或 2 次的不定積分, 受興趣使然, 筆者查詢了探討 $n$ 次反三角函數積分相關的文獻後發現相關研究甚少, 僅有一篇給出其遞迴形式的貼文 貳、文獻探討對於 $n=1$ 的情況, 可通過分部積分法解決 一、反正弦函數 $\arcsin(x)$ 之不定積分\begin{align*} \int\arcsin(x)\text{d}x &=x\cdot\arcsin(x)-\int x\mathrm{d}(\arcsin(x))\\ &=x\cdot\arcsin(x)-\int \sin\left(\arcsin(x)\right)\mathrm{d}(\arcsin(x))\\ &=x\cdot\arcsin(x)+\cos\left(\arcsin(x)\right)+C. \end{align*} 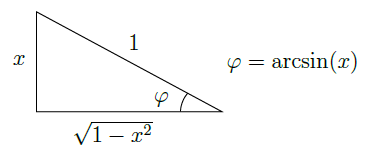 由圖可知, \begin{align*} \int\arcsin(x)\text{d}x=x\cdot\arcsin(x)+\sqrt{1-x^2}+C. \end{align*} 二、反餘弦函數 $\arccos(x)$之不定積分\begin{align*} \int\arccos(x)\text{d}x &=x\cdot\arccos(x)-\int x\mathrm{d}(\arccos(x))\\ &=x\cdot\arccos(x)-\int\cos(\arccos(x))\mathrm{d}(\arccos(x))\\ &=x\cdot\arccos(x)-\sin(\arccos(x))+C. \end{align*} 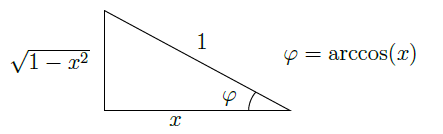 由圖可知, \begin{align*} \int\arccos(x)\text{d}x=x\cdot\arccos(x)-\sqrt{1-x^2}+C. \end{align*} 參、研究分析與結果對於下文 【定理 1】 和 【定理 3】 我們可採取兩種方法求得: 定理 1: $$\int\arcsin^n(x)\mathrm{d}x=\sum_{i=0}^nP_{i}^{n}\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)\left(\arcsin(x)\right)^{n-i}+C.$$ 證明: (一)、 方法一 \begin{align*} I &= \int\arcsin^n(x)\mathrm{d}x\\ &= x\cdot\arcsin^n(x)-n\int x\arcsin^{n-1}(x)\mathrm{d}\left(\arcsin(x)\right). \end{align*} 令 $\varphi=\arcsin(x)$並運用分部積分: \begin{align*} I &=x\cdot\arcsin^n(x)-n\int\sin(\varphi)\cdot \varphi^{n-1}\mathrm{d}\varphi\\ &=x\cdot\arcsin^n(x)+n\int\varphi^{n-1}\mathrm{d}\left(\cos\varphi\right)\\ &=x\cdot\arcsin^n(x)+n\varphi^{n-1}\cos\varphi-n(n-1)\int\varphi^{n-2}\mathrm{d}\left(\sin\varphi\right)\\ &=x\cdot\arcsin^n(x)+n\varphi^{n-1}\cos\varphi\!-\!n(n\!-\!1)\varphi^{n-2} \sin\varphi\!-\!n(n\!-\!1)(n\!-\!2)\!\int\varphi^{n-3}\mathrm{d}(\cos\varphi)\\ &=x\cdot\arcsin^n(x)+n\varphi^{n-1}\cos\varphi-n(n-1)\varphi^{n-2} \sin\varphi-n(n-1)(n-2)\varphi^{n-3}\cos\varphi\\ &\quad\ +n(n-1)(n-2)(n-3)\int\varphi^{n-4}\mathrm{d}(\sin\varphi)\\ &=\cdots\\ &=x\cdot\arcsin^n(x)+\displaystyle\sum_{i=1}^nP_{i}^n\sin(\varphi+\frac{i\pi}{2})\cdot\varphi^{n-i}+C\\ &=\displaystyle\sum_{i=0}^nP_{i}^{n}\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)\left(\arcsin(x)\right)^{n-i}+C. \end{align*} (二)、方法二 \begin{align*} I_n &=\int\arcsin^n(x)\mathrm{d}x\\ &=x\arcsin^n(x)-n\int\arcsin^{n-1}(x)\cdot\frac{x}{\sqrt{1-x^2}}\mathrm{d}x \end{align*} 注意到: \begin{align*} \int\frac{x}{\sqrt{1-x^2}}\mathrm{d}x & \overset{t=1-x^2}{=} -\frac12\int\frac1{\sqrt{t}}\mathrm{d}t\\ &=-\sqrt{t}+C\\ &=-\sqrt{1-x^2}+C. \end{align*} 因此: \begin{align*} I_n &=x\arcsin^n(x)+n\int\arcsin^{n-1}(x)\mathrm{d}(\sqrt{1-x^2})\\ &=x\arcsin^n(x)+n\arcsin^{n-1}(x)\sqrt{1-x^2}-n\int\sqrt{1-x^2}\mathrm{d}(\arcsin^{n-1}(x))\\ &=x\arcsin^n(x)+n\arcsin^{n-1}(x)\sqrt{1-x^2}-n\int\sqrt{1-x^2}\cdot\frac{(n-1)\arcsin^{n-2}(x)}{\sqrt{1-x^2}}\mathrm{d}x\\ &=x\arcsin^n(x)+n\arcsin^{n-1}(x)\sqrt{1-x^2}-n(n-1)\int\arcsin^{n-2}(x)\mathrm{d}x\\ &=x\arcsin^n(x)+n\arcsin^{n-1}(x)\sqrt{1-x^2}-n(n-1)I_{n-2}. \end{align*} 至此, 我們得到了關於 $I_n$ 的二階遞迴式, 我們可以反復遞迴以正向求解, 也可利用此式結合數學歸納法證明結論。 我們先嘗試正向求解: \begin{align*} I_n&=x\arcsin^n(x)+n\arcsin^{n-1}(x)\sqrt{1-x^2}-n(n-1)[x\arcsin^{n-2}(x)+\\ &\quad(n-2)\sqrt{1-x^2}\arcsin^{n-3}(x)-(n-2)(n-3)I_{n-4}]\\ &=\sin(\arcsin(x))\arcsin^n(x)+n\sin(\arcsin(x)+\frac{\pi}2)\arcsin^{n-1}(x)\\ &\quad+n(n-1)\sin(\arcsin(x)+\pi)\arcsin^{n-2}(x)\\ &\quad +n(n-1)(n-2)\sin(\arcsin(x)+\frac{3\pi}2)+\cdots\\ &=\sum_{i=0}^nP_{i}^{n}\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)\left(\arcsin(x)\right)^{n-i}+C. \end{align*} 相應的, 我們嘗試利用數學歸納法: 當 $n=1$ 時, 由文獻探討中的計算, 我們知道: $$\int\arcsin(x)\text{d}x=x\cdot\arcsin(x)+\sqrt{1-x^2}+C,$$ 而 \begin{align*} I_1&=\sum_{i=0}^1P_i^1\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)(\arcsin(x))^{1-i}+C\\ &=\sin\left(\arcsin(x)\right)\cdot\arcsin(x)+\sin\left(\arcsin(x)+\frac{\pi}{2}\right)+C\\ &=x\cdot\arcsin(x)+\cos\left(\arcsin(x)\right)+C\\ &=x\cdot\arcsin(x)+\sqrt{1-x^2}+C, \end{align*} 即 $n=1$ 時結論成立。 當 $n=2$ 時, 由上文的二階遞迴式我們得到: \begin{align*} \int\arcsin^2(x)\text{d}x&= x\arcsin^2(x)+2\sqrt{1-x^2}\arcsin(x)-2I_{0}\\ &=x\arcsin^2(x)+2\sqrt{1-x^2}\arcsin(x)-2x+C, \end{align*} 而 \begin{align*} I_2&=\sum_{i=0}^2P_i^2\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)(\arcsin(x))^{2-i}+C\\ &=\sin\left(\arcsin(x)\right)\arcsin^2(x) +2\sin\left(\arcsin(x)+\frac{\pi}{2}\right)\arcsin(x)\\ &\quad +2\sin\left(\arcsin(x)+\pi\right)+C\\ &=x\arcsin^2(x)+2\sqrt{1-x^2}\arcsin(x)-2x+C, \end{align*} 即 $n=2$ 時結論也成立。 假設 $n=k-2$ 時結論成立, 即 $$I_{k-2}=\sum_{i=0}^{k-2}P_i^{k-2}\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)(\arcsin(x))^{k-2-i}+C.$$ 結合上文的二階遞迴式, 我們有 \begin{align*} I_k&=x\arcsin^k(x)+k\arcsin^{k-1}(x)\sqrt{1-x^2}-k(k-1)I_{k-2}\\ &=x\arcsin^k(x)+k\arcsin^{k-1}(x)\sqrt{1-x^2}\\ &\ \ \ -k(k-1)\sum_{i=0}^{k-2}P_i^{k-2}\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)(\arcsin(x))^{k-2-i}+C\\ &=x\arcsin^k(x)+k\arcsin^{k-1}(x)\sqrt{1-x^2}\\ &\quad +\sum_{i=0}^{k-2}P_{i+2}^{k}\sin\left(\arcsin(x)+\frac{(i+2)\pi}{2}\right)(\arcsin(x))^{k-(i+2)}+C\\ &=x\arcsin^k(x)+k\arcsin^{k-1}(x)\sqrt{1-x^2}\\ &\quad+\sum_{i=2}^kP_i^k\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)(\arcsin(x))^{k-i}+C\\ &=\sum_{i=0}^kP_i^k\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)(\arcsin(x))^{k-i}+C. \end{align*} 即若 $n=k-2$ 時結論成立, 則 $n=k$ 時結論亦成立, 又 $n=1,2$ 時結論成立, 我們可以得到 $\forall n\in\mathbb{N}$, 結論皆成立。 定理 2: $$\int\arcsin^n(\frac{x}{a})\mathrm{d}x=a\cdot\sum_{i=0}^nP_i^n\sin\left(\arcsin(\frac{x}{a})+\frac{i\pi}{2}\right)(\arcsin(\frac{x}{a}))^{n-i}+C.$$ 證明: \begin{align*} I&=\int\arcsin^n(\frac{x}{a})\mathrm{d}x\\ &=a\cdot\int\arcsin^n(\frac{x}{a})\mathrm{d}(\frac{x}{a})\\ &=\displaystyle a\cdot\sum_{i=0}^nP_i^n\sin\left(\arcsin(\frac{x}{a})+\frac{i\pi}{2}\right)(\arcsin(\frac{x}{a}))^{n-i}+C. \end{align*} 定理 3: $$\int\arccos^n(x)\mathrm{d}x=\sum_{i=0}^nP_i^n\cos\left(\arccos(x)+\frac{i\pi}{2}\right)(\arccos(x))^{n-i}+C.$$ 證明: (一)、方法一 \begin{align*} I &=\int\arccos^n(x)\mathrm{d}x\\ &=x\cdot\arccos^n(x)-n\int x\arccos^{n-1}(x)\mathrm{d}(\arccos(x)). \end{align*} 令 $\varphi=\arccos(x)$ 並運用分部積分: \begin{align*} I &=x\cdot\arccos^n(x)-n\int\cos(\varphi)\cdot\varphi^{n-1}\mathrm{d}\varphi\\ &=x\cdot\arccos^n(x)-n\int\varphi^{n-1}\mathrm{d}(\sin\varphi)\\ &=x\cdot\arccos^n(x)-n\varphi^{n-1}\sin\varphi-n(n-1)\int\varphi^{n-2}\mathrm{d}(\cos\varphi)\\ &=x\cdot\arccos^n(x)-n\varphi^{n-1}\sin\varphi-n(n-1)\varphi^{n-2}\cos\varphi+\\ &\quad n(n-1)(n-2)\int\varphi^{n-3}\mathrm{d}(\sin\varphi)\\ &=\cdots\\ &=x\cdot\arccos^n(x)+\sum_{i=1}^nP_i^n\cos(\varphi+\frac{i\pi}{2})\cdot\varphi^{n-i}+C\\ &=x\cdot\arccos^n(x)+\sum_{i=1}^nP_i^n\cos\left(\arccos(x)+\frac{i\pi}{2}\right)\cdot(\arccos(x))^{n-i}+C\\ &=\sum_{i=0}^nP_i^n\cos\left(\arccos(x)+\frac{i\pi}{2}\right)(\arccos(x))^{n-i}+C. \end{align*} (二)、方法二 \begin{align*} I_n &=\int\arccos^n(x)\mathrm{d}x\\ &=x\arccos^n(x)+n\int\arccos^{n-1}(x)\cdot\frac{x}{\sqrt{1-x^2}}\mathrm{d}x. \end{align*} 我們知道: \begin{align*} \int\frac{x}{\sqrt{1-x^2}}\mathrm{d}x &=-\sqrt{1-x^2}+C. \end{align*} 因此: \begin{align*} I_n &=x\arccos^n(x)\!-\!n\int\arccos^{n-1}(x)\mathrm{d}(\sqrt{1-x^2})\\ &=x\arccos^n(x)\!-\!n\arccos^{n-1}(x)\sqrt{1\!-\!x^2}\!+\!n\!\int\!\sqrt{1\!-\!x^2}\mathrm{d}(\arccos^{n-1}(x))\\ &=x\arccos^n(x)\!-\!n\arccos^{n-1}(x)\sqrt{1\!-\!x^2}\!-\!n\int\sqrt{1\!-\!x^2} \cdot\frac{(n\!-\!1)\arccos^{n-2}(x)}{\sqrt{1\!-\!x^2}}\mathrm{d}x\\ &=x\arccos^n(x)\!-\!n\arccos^{n-1}(x)\sqrt{1\!-\!x^2}\!-\!n(n-1)\!\int\arccos^{n-2}\!(x)\mathrm{d}x\\ &=x\arccos^n(x)\!-\!n\arccos^{n-1}(x)\sqrt{1\!-\!x^2}\!-\!n(n-1)I_{n-2}. \end{align*} 至此, 我們得到了關於$I_n$的二階遞迴式, 類似的, 我們可以反復遞迴以正向求解, 也可利用此式結合數學歸納法, 而後者在前文已介紹, 此處不再贅述。 \begin{align*} I_n&=x\arccos^n(x)-n\arccos^{n-1}(x)\sqrt{1-x^2}-n(n-1)[x\arccos^{n-2}(x)-\\ &\quad(n-2)\sqrt{1-x^2}\arccos^{n-3}(x)-(n-2)(n-3)I_{n-4}]\\ &=\cos(\arccos(x))\arccos^n(x)+n\cos(\arccos(x)+\frac{\pi}2)\arccos^{n-1}(x)\\ &\quad+n(n-1)\cos(\arccos(x)+\pi)\arccos^{n-2}(x)\\ &\quad+n(n-1)(n-2)\cos(\arccos(x)+\frac{3\pi}2)+\cdots\\ &=\sum_{i=0}^nP_{i}^{n}\cos\left(\arccos(x)+\frac{i\pi}{2}\right)\left(\arccos(x)\right)^{n-i}+C. \end{align*} 定理 4: $$\int\arccos^n(\frac{x}{a})\mathrm{d}x=a\cdot\sum_{i=0}^nP_i^n\cos\left(\arccos(\frac{x}{a})+\frac{i\pi}{2}\right)(\arccos(\frac{x}{a}))^{n-i}+C.$$ 證明: \begin{align*} I&=\int\arccos^n(\frac{x}{a})\mathrm{d}x\\ &=a\cdot\int\arccos^n(\frac{x}{a})\mathrm{d}(\frac{x}{a})\\ &=a\cdot\sum_{i=0}^nP_i^n\cos\left(\arccos(\frac{x}{a})+\frac{i\pi}{2}\right)(\arccos(\frac{x}{a}))^{n-i}+C. \end{align*} 對於定理 3 和定理 4, 我們運用換元、 分部積分後結合 Fubini-Tonelli 定理將求和與積分換序進而求解。 定理 5: $$\int x^{2n}\arcsin(x)\mathrm{d}x =\frac{x^{2n+1}\arcsin(x)}{2n+1}+\frac{1}{2n+1}\sum_{i=0}^nC_i^n\frac{(-1)^i}{2i+1}(1-x^2)^{i+\frac12}+C.$$ 證明: \begin{align*} I_{2n} &=\int x^{2n}\arcsin(x)\mathrm{d}x\\ &=\frac{1}{2n+1}\int\arcsin(x)\mathrm{d}(x^{2n+1})\\ &=\frac{x^{2n+1}\arcsin(x)}{2n+1}-\frac{1}{2n+1}\int x^{2n+1}\mathrm{d}(\arcsin(x)). \end{align*} 令 $\varphi=\arcsin(x)$, \begin{align*} I_{2n} &=\frac{x^{2n+1}\arcsin(x)}{2n+1}-\frac1{2n+1}\int\sin^{2n+1}\varphi\mathrm{d}\varphi\\ &=\frac{x^{2n+1}\arcsin(x)}{2n+1}+\frac1{2n+1}\int\sin^{2n}\varphi\mathrm{d}(\cos\varphi). \end{align*} 令 $t=\cos\varphi=\cos\left(\arcsin(x)\right)=\sqrt{1-x^2}$, \begin{align*} I_{2n} &=\frac{x^{2n+1}\arcsin(x)}{2n+1}+\frac1{2n+1}\int(1-t^2)^n\mathrm{d}t\\ &=\frac{x^{2n+1}\arcsin(x)}{2n+1}+\frac1{2n+1}\int\sum_{i=0}^nC_i^n(-t^2)^i\mathrm{d}t.\tag{*} \end{align*} 注意到: \begin{align*} \sum_{i=0}^nC_i^n\int t^{2i}\mathrm{d}t &=\sum_{i=0}^nC_i^n\cdot\frac1{2i+1}t^{2i+1}+C\\ &=\sum_{i=0}^nC_i^n\cdot\frac1{2i+1}(1-x^2)^{i+\frac12}+C\\ &\lt\infty. \end{align*} 因此, 由 Fubini-Tonelli 定理 \begin{align*} I_{2n} &=\frac{x^{2n+1}\arcsin(x)}{2n+1}+\frac1{2n+1}\sum_{i=0}^nC_i^n\int(-t^2)^i\mathrm{d}t\\ &=\frac{x^{2n+1}\arcsin(x)}{2n+1}+\frac1{2n+1}\sum_{i=0}^nC_i^n\frac{(-1)^i}{2i+1}t^{2i+1}+C\\ &=\frac{x^{2n+1}\arcsin(x)}{2n+1}+\frac{1}{2n+1}\sum_{i=0}^nC_i^n\frac{(-1)^i}{2i+1}(1-x^2)^{i+\frac12}+C. \end{align*} 定理 6: $$\int x^{2n}\arccos(x)\mathrm{d}x =\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac{1}{2n+1}\sum_{i=0}^nC_i^n\frac{(-1)^i}{2i+1}(1-x^2)^{i+\frac12}+C.$$ 證明: \begin{align*} I_{2n} &=\int x^{2n}\arccos(x)\mathrm{d}x\\ &=\frac{1}{2n+1}\int\arccos(x)\mathrm{d}(x^{2n+1})\\ &=\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac{1}{2n+1}\int x^{2n+1}\mathrm{d}(\arccos(x)). \end{align*} 令 $\varphi=\arccos(x)$, \begin{align*} I_{2n} &=\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac1{2n+1}\int\cos^{2n+1}\varphi\mathrm{d}\varphi\\ &=\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac1{2n+1}\int\cos^{2n}\varphi\mathrm{d}(\sin\varphi). \end{align*} 令 $t=\sin\varphi=\sin\left(\arccos(x)\right)=\sqrt{1-x^2}$, \begin{align*} I_{2n} &=\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac1{2n+1}\int(1-t^2)^n\mathrm{d}t\\ &=\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac1{2n+1}\int\sum_{i=0}^nC_i^n(-t^2)^i\mathrm{d}t.\tag{**} \end{align*} 注意到: \begin{align*} \sum_{i=0}^nC_i^n\int t^{2i}\mathrm{d}t &=\sum_{i=0}^nC_i^n\cdot\frac1{2i+1}t^{2i+1}+C\\ &=\sum_{i=0}^nC_i^n\cdot\frac1{2i+1}(1-x^2)^{i+\frac12}+C\\ &\lt\infty. \end{align*} 因此, 由 Fubini-Tonelli 定理, $(**)$ 式中的求和與積分順序可以互換: \begin{align*} I_{2n} &=\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac1{2n+1}\sum_{i=0}^nC_i^n\int(-t^2)^i\mathrm{d}t\\ &=\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac1{2n+1}\sum_{i=0}^nC_i^n\frac{(-1)^i}{2i+1}t^{2i+1}+C\\ &=\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac{1}{2n+1}\sum_{i=0}^nC_i^n\frac{(-1)^i}{2i+1}(1-x^2)^{i+\frac12}+C. \end{align*} 肆、研究結論本文推導得出了 $\forall n\in\mathbb{N}$ 的以下六則公式: \begin{align*} &\int\arcsin^n(x)\mathrm{d}x=\sum_{i=0}^nP_{i}^{n}\sin\left(\arcsin(x)+\frac{i\pi}{2}\right)\left(\arcsin(x)\right)^{n-i}+C,\\ &\int\arcsin^n(\frac{x}{a})\mathrm{d}x=a\cdot\sum_{i=0}^nP_i^n\sin\left(\arcsin(\frac{x}{a})+\frac{i\pi}{2}\right)(\arcsin(\frac{x}{a}))^{n-i}+C,\\ &\int\arccos^n(x)\mathrm{d}x=\sum_{i=0}^nP_i^n\cos\left(\arccos(x)+\frac{i\pi}{2}\right)(\arccos(x))^{n-i}+C,\\ &\int\arccos^n(\frac{x}{a})\mathrm{d}x=a\cdot\sum_{i=0}^nP_i^n\cos\left(\arccos(\frac{x}{a})+\frac{i\pi}{2}\right)(\arccos(\frac{x}{a}))^{n-i}+C,\\ &\int x^{2n}\arcsin(x)\mathrm{d}x =\frac{x^{2n+1}\arcsin(x)}{2n+1}+\frac{1}{2n+1}\sum_{i=0}^nC_i^n\frac{(-1)^i}{2i+1}(1-x^2)^{i+\frac12}+C,\\ &\int x^{2n}\arccos(x)\mathrm{d}x =\frac{x^{2n+1}\arccos(x)}{2n+1}-\frac{1}{2n+1}\sum_{i=0}^nC_i^n\frac{(-1)^i}{2i+1}(1-x^2)^{i+\frac12}+C. \end{align*} 對於其延伸性問題, 如 $n$ 次反正切與反餘切, 反正割與反餘割函數之不定積分, 都將是筆者未來繼續研究的方向。 參考文獻本文作者投稿時就讀華東台商子女學校 |
| 頁碼 | 91-101 |
2025年6月 49卷2期
$n$ 次反三角函數之不定積分

