2006年9月, 項武義先生在臺大數學系演講「三體問題」。
演講開始時, 項先生先提到密度均勻的球體對球體外一點 $P$ 的(萬有)引力可以看成是質量全部集中在球心後,
球心對 $P$ 點的引力。眾所周知, 這是一個有相當難度的積分問題, 並且是一個當年困擾牛頓的問題。
許多文獻都談到這是牛頓遲遲不願發表萬有引力原理的原因之一。
舉例言之, 1962年出版, 由 D. Halliday 和 R. Resnick 合著的物理教科書在319頁有這樣一段評論:
1. 項武義提出的證明
項先生在演講當天對牛頓的結論給了一個有別於曹先生書中的證明。
但是由於項先生的目的只是先行?明為什麼在討論二體、三體或多體問題時可以把星球看成一點, 所以證明有些簡略。
項先生所言大抵如下:
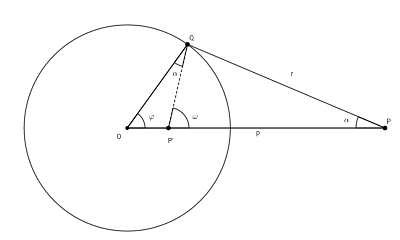
圖一
如圖, 不妨假設只積一個半徑為1的球面(或球殼), 剖面是一個圓 $\overline{OP}=p$, 另取 $p'$ 點,
使 $\overline{OP'}=\frac {1}{p}$, 不難看出 $\triangle OPQ$ 和 $\triangle OQP'$ 相似, 因此 $\angle OQP'=\angle OPQ=\alpha$。
現考慮在 $Q$ 點的面積 元素 $dA$, $dA$ 對 $P$ 的引力是(差一個常數) $dA/r^{2}$, 又因球對稱, 只需考慮沿 $OP$ 的向心方向,
所以是 $dA\cos\alpha/r^{2}$。
由於 $\angle OQP'=\alpha$, 由(微觀的)投影關係 $dA\cos\alpha$ 可以看成是以 $P'$ 為心,
沿 $P'Q$ 方向的面積 元素, 因此有
$$
dA\cos\alpha=d\sigma\cdot{\overline{P'Q}}^{2}
$$
式中 $d\sigma$ 代表半徑為1的球面面積 元素。又由相似三角形的比例關係而有
\begin{eqnarray*}
\overline{P'Q}/r&=&\frac {1}{\overline{OP}}\\
{\hbox {或}}
{\overline{P'Q}}^{2}/r^{2}&=&\frac {1}{p^{2}}
\end{eqnarray*}
因此
$$dA\cos\alpha/r^{2}=d\sigma\cdot{\overline{P'Q}}^{2}/r^{2}=d\sigma/p^{2}$$
所以
$$\int dA\cos\alpha/r^{2}=\int d\sigma/p^{2}=\frac {1}{p^{2}}\int d\sigma=\frac {1}{p^{2}}\cdot 4\pi$$
定理證畢。
項先生的證明雖然簡略, 但是因為從幾何入手, 直觀上比較自然, 唯一需要多所著墨的是從微觀投影關係得出的等式
$$
dA\cos\alpha=d\sigma\cdot{\overline{P'Q}}^{2}
$$
2. 嚴格的證明
如圖(單位球面)
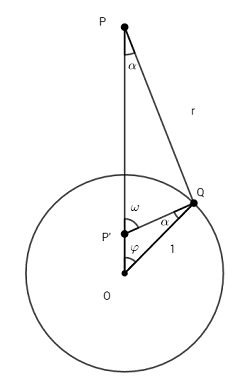
圖二
要計算的積分是($\varphi$, $\theta$ 是球面坐標 $0\le\varphi\le\pi$, $\theta$ 省略, $0\le\theta\le 2\pi$,
$\overline{OP}=p$, $\overline{OP'}=\frac {1}{p}$, $\overline{PQ}=r$, $\overline{OQ}=1$)
$$
\int^{2\pi}_{\theta=0}\int^{\pi}_{\varphi=0}\frac {\cos\alpha}{r^{2}}\sin\varphi\ d\varphi\ d\theta
=2\pi\int^{\pi}_{\varphi=0}\frac {\cos\alpha}{r^{2}}\sin\varphi\ d\varphi
$$
因為 $$\frac {r}{\overline{P'Q}}=\frac {\overline{OP}}{1}=p$$
積分式變成 $$\frac {2\pi}{p^{2}}\int^{\pi}_{\varphi=0}\frac {\cos\alpha}{{\overline{P'Q}}^{2}}\sin\varphi\ d\varphi$$
在被積分的式子裡, 不難看出 $\sin\varphi=\overline{P'Q}\sin\omega$, 因此如果能夠證明
$$
\cos\alpha\ d\varphi=\overline{P'Q}d\omega
$$
再將此代入積分, 就可以得到
$$
\frac {2\pi}{p^{2}}\int^{\pi}_{\varphi=0}\frac {{\overline{P'Q}}^{2}\sin\omega\ d\omega}{{\overline{P'Q}}^{2}}
=\frac {2\pi}{p^{2}}\int^{\pi}_{\varphi=0}\sin\omega\ d\omega=\frac {4\pi}{p^{2}}
$$
此處注意到 $\cos\alpha\ d\varphi=\overline{P'Q}d\omega$ 其實是說明以 $\overline{P'Q}$ 為半徑對應的弧長
$\overline{P'Q}d\omega$ 和 $d\varphi$ 之間的微觀投影關係, 易見此一等式和上一節中的微觀面積 投影關係
$dA\cos\alpha=d\sigma{\overline{P'Q}}^{2}$ 等價。(註三)
上述一維的微觀投影關係 $\cos\alpha\ d\varphi=\overline{P'Q}d\omega$ 如果要嚴格的證明, 必須利用極限求出
$d\omega/d\varphi=\frac {\cos\alpha}{\overline{P'Q}}$。
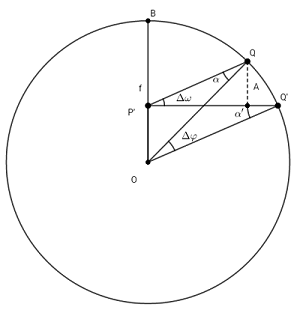
現在, 在圖二中, 作 $\Delta\varphi$ 和 $\Delta\omega$ 的對應圖
圖三
並由 $Q$ 向 $P'Q'$ 作垂線段, 垂足為 $A$, 則
$$
\frac {\overline{P'Q}\Delta\omega}{\Delta\varphi}
=\frac {\overline{P'Q}\Delta\omega}{\overline{QA}}\ \ \frac {\overline{QA}}{\overline{QQ'}}\ \ \frac {\overline{QQ'}}{\Delta\varphi}
$$
當 $Q'\rightarrow Q$ 時,
(1) 注意到 $\overline{OQ'}$ 是半徑, $Q'\rightarrow Q$ 時, ${\alpha}'+\angle QQ'A\rightarrow \frac {\pi}{2}$,
${\alpha}'\rightarrow\alpha$, 所以 $\overline{QA}/\overline{QQ'}=\sin\angle QQ'A\rightarrow\cos\alpha$。
(2) $\overline{QQ'}/\Delta\varphi\rightarrow 1$, 因為 $\overline{OQ'}=\overline{OQ}=\hbox{半徑}=1$。
(3) $\displaystyle\frac {\overline{P'Q}\Delta\omega}{\overline{QA}}=\displaystyle\frac {\overline{P'Q}\Delta\omega}{\overline{P'Q}\sin\Delta\omega}\rightarrow 1$。
(1) (2) (3) 相乘得到
$$
\frac {\overline{P'Q}\Delta\omega}{\Delta\varphi}\rightarrow\cos\alpha,\hbox{ 亦即 }\overline{P'Q}d\omega=\cos\alpha\ d\varphi.
$$
3. 《原理》的幾何證明
前文提到 Halliday 和 Resnick 對牛頓積分問題的評論, 評論指出只有利用微積分,
才能嚴格證明「密度均勻的球體對球體外一點 的(萬有)引力可以看成是質量全部集中在球心」。
回到1687年出版的《自然哲學之數學原理》, 在第十二章的命題71, 牛頓談到:
《在相同的條件下, 球面外的小球受到指向球面中心的吸引力反比於小球到該中心距離的平方》(中譯本182頁)。
本命題只論球面, 因為球面的情形比球體的情形更為基本; 奇妙的是, 牛頓在證明本命題的時候,
大部分的想法均源自幾何, 只有在討論某些微量之間的比例時, 才隱約用到求極限的方法;
想來牛頓之所以避免使用微積分可能是因為在《原理》出版的時代, 微積分並非顯學。
身為微積分發明人之一的牛頓, 為了提高《原理》一書的可讀性, 採取了當時科學家共通的語言---歐氏幾何。
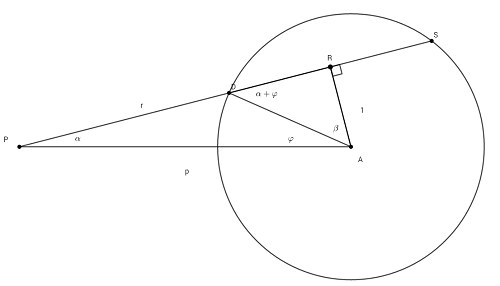
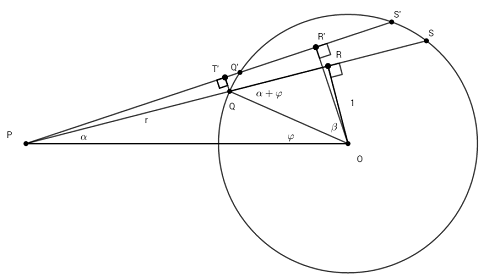
本文在此不擬複製《原理》命題71的證明, 但是願意以微積分的語言重現牛頓的幾何想法, 請看圖四(圖中, $\overline{PQ}=r$,
$\overline{OQ}=1$, $\overline{OR}\bot\overline{QS}$, $\overline{OR}=l$, $\overline{OP}=p$, $\angle QOR=\beta$)。
圖四
積分的式子如前:
$$
\int\frac {\cos\alpha\ \sin\varphi\ d\varphi}{r^{2}}
$$
牛頓的想法是將 $\alpha$, $\varphi$, $r$ 以 $l$ 表達, 並找出相關的微量關係, 因此必須先將
$l$ 變化到 $l+\Delta l$, 如圖五。(圖中 $\overline{OR'}\bot\overline{Q'S'}$, $\overline{OR'}=l+\Delta l$,
$\overline{OR'}$ 和 $\overline{QS}$ 交於 $F$)
圖五
作 $\overline{QT'}$ 垂直 $\overline{PQ'}$, 垂足為 $T'$。以下的論證多從比例入手;
論證中涉及取極限 $Q'\rightarrow Q$ 之後方能成立的等式皆以近似等號 $\approx$ 表示;
論證分為五個步驟。
(一) $\angle QQ'T'$ 在近似之下是一個弦切角, 因此 $\angle QQ'T'=\pi-\angle QQ'O-\angle OQ'R'
\approx\pi-\frac {\pi}{2}-\angle OQF=\frac {\pi}{2}-(\alpha+\varphi)=\beta$(圖四)$\\$
所以有 $\overline{QT'}=\overline{QQ'}\sin\angle QQ'T'\approx\overline{QQ'}\sin\beta\approx\Delta\varphi\ \sin\beta$(圖五), 或
$\Delta\varphi\approx\overline{QT'}/\sin\beta$。
(二) $\overline{QT'}/\overline{FR'}=\overline{PQ}/\overline{PF}$, 但是因為 $\overline{FR'}\approx\Delta l$,
$\overline{PF}\approx\overline{PR}$$\\$
所以有 $\overline{QT'}=\overline{FR'}(\overline{PQ}/\overline{PF})\approx\frac {\overline{PQ}}{\overline{PR}}\Delta l
=\frac {r}{p\cos\alpha}\Delta l$(圖五)。
(三) $\sin\varphi=r\sin\alpha=r l/p$(圖四)。
(四) $\sin\beta=\sqrt{1-l^{2}}$(圖四)。
(五) 將(一), (二), (三), (四)的結果代入積分式, 得到
\begin{eqnarray*}
&&\frac {\cos\alpha\ \sin\varphi\ d\varphi}{r^{2}}\approx\frac {\cos\alpha\ \Delta\varphi}{r^{2}}\frac {rl}{p}\hbox{ (根據(三) ) }\\
&&\approx\frac {l\cos\alpha}{rp}\frac {\overline{QT'}}{\sin\beta}\hbox{ (根據(一)) }\\
&&\approx\frac {l\cos\alpha}{rp}\frac {r}{p\cos\alpha}\frac {\Delta l}{\sin\beta}\hbox{ (根據(二)) }
=\frac {1}{p^{2}}\frac {l\Delta l}{\sin\beta}=\frac {1}{p^{2}}\frac {l\Delta l}{\sqrt{1-l^{2}}}\hbox{ (根據(四))。 }
\end{eqnarray*}
從(一)至(五)的討論可知 $\int\frac {\cos\alpha\ \sin\varphi\ d\varphi}{r^{2}}=\frac {1}{p^{2}}\int\frac {l\ dl}{\sqrt{1-l^{2}}}$ 易見
$\int\frac {l\ dl}{\sqrt{1-l^{2}}}$ 是一個定值, 所以積分與 $p^{2}$ 成反比(註四)。
最後補充一點, 上式的右邊 $\int\frac {l\ dl}{\sqrt{1-l^{2}}}$ 應該解釋為 $\int^{1}_{0}\frac {l\ dl}{\sqrt{1-l^{2}}}$
的兩倍, 這是因為 $\varphi$ 對到 $l$ 是二對一的緣故; 計算 $\frac {2}{p^{2}}\int^{1}_{0}\frac {l\ dl}{\sqrt{1-l^{2}}}$, 得值
$\frac {2}{p^{2}}$, 所以 $2\pi\int\frac {\cos\alpha\ \sin\varphi\ d\varphi}{r^{2}}=\frac {4\pi}{p^{2}}$,
表示球面的引力確可以看成「質量全部集中在球心」。(註五)
註一. 牛頓在1687年出版《自然哲學之數學原理》(The Mathematical Principles of Natural Philosophy 或 Principia)。
出版時的標題為 Philosophiae naturalis principia mathematica.
中譯本於2005年2月由台北大塊文化出版, 譯者是王克迪先生。有關本文談到的問題請見中譯本第十二章《球體的吸引力》。
註二. 曹亮吉在所著微積分 $15.24\sim15.25$ 呈現的計算如下(圖中 $\rho$, $\varphi$, $\theta$ 是球坐標
$0\le\varphi\le\pi$ ,$0\le\theta\le 2\pi$, $\overline{OP}=p$, $\overline{PQ}=r$, $\overline{OQ}=\rho$):
註三. 如果 $\cos\alpha\ d\varphi=\overline{P'Q}d\omega$, 則
\begin{eqnarray*}
\cos\alpha\ dA&=&\cos\alpha\sin\varphi\ d\varphi\ d\theta\\
&=&\overline{P'Q}\sin\varphi\ d\omega\ d\theta\\
&=&\overline{P'Q}\,\overline{P'Q}\sin\omega\ d\omega\ d\theta\\
&=&{\overline{P'Q}}^{2}\sin\omega\ d\omega\ d\theta
\end{eqnarray*}
式中 $\sin\omega\ d\omega\ d\theta$ 就是第二節中的 $d\sigma$。
註四.《原理》證明的關鍵在於由(一)、(二)兩個步驟得出的結論
$$
\Delta\varphi\sin\beta\approx\frac {r}{p\cos\alpha}\Delta l
$$
此式相當於微分關係式 $d\varphi\sin\beta=\frac {r}{p\cos\alpha}dl$, 以下是嚴格的證明(圖四)
由 $l=\cos\beta=p\sin\alpha$, 得 $dl=-\sin\beta\ d\beta=p\cos\alpha\ d\alpha$, 但因 $(\alpha+\varphi)+\beta=\frac {\pi}{2}$,
所以 $\sin\beta(d\varphi+d\alpha)=-\sin\beta\ d\beta=p\cos\alpha\ d\alpha$ 或 $\sin\beta\ d\varphi=(p\cos\alpha-\sin\beta)d\alpha=r\ d\alpha$,
又因為 $\frac {r}{p\cos\alpha}dl=\frac {r}{p\cos\alpha}p\cos\alpha\ d\alpha=r\ d\alpha$, 可得 $\sin\beta\ d\varphi=\frac {r}{p\cos\alpha}dl$,
微分關係式得證
<>
歡迎讀者比較"幾何的"證明(如 (一) 、(二))和"微分的"證明(如本註四)。
註五. 積分的目的是要求總量 $I$, 方法是以微量 $dI$ 求和而寫下積分式
$$
\int dI
$$
若要計算上式, 必須選擇適當的參數 $t$, 再將積分式表為
$$
\int \frac {dI}{dt}dt
$$
亦即從 $\frac {dI}{dt}$ 得回 $I$, 此一過程稱為微積分基本定理。
本文的註二選擇 $r$ 為積分參數, 但在本文第三節中重現《原理》的計算過程則是選擇 $l$ 為積分參數, 兩者各擅勝場。
---本文作者為台大數學系退休教授---